
科目: 来源: 题型:
【题目】在 Rt△ABC 中,∠BAC=90°,AC=AB,点 F 是射线 CA 上一点,连接 BF,过 C 作 CE⊥BF,垂足为点 E,直线 CE,AB 相交于点 D.
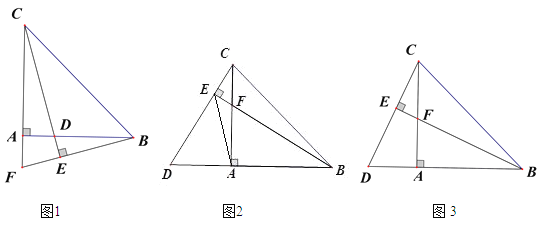
(1)如图 1,当点 F 在线段 CA 延长线上时,求证:AB+AD=CF;
(2)如图 2,当点 F 在线段 CA 上时,连接 EA,求证:EA 平分∠DEB;
(3)如图 3,当点 F 恰好为线段 CA 的中点时,EF=1,试求△BDE 的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】抛物线y= ax2+bx+c经过A(1,4)、B(-1,0)、C(-2,5)三点
(1)求抛物线的解析式并画出这条抛物线;
(2)直角坐标系中点的横坐标与纵坐标均为整数的点称为整点。试结合图象,写出在第四象限内抛物线上的所有整点的坐标。
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系 xoy 中,已知点 A 的坐标为(-2,0).
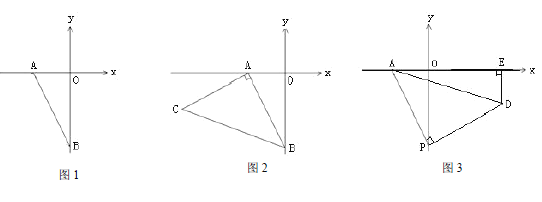
(1)如图 1,当点 B 的坐标为(0,-4)时,则△AOB 的面积是 ;
(2)如图 2,在(1)的条件下,过点 A 作 AC⊥AB,且使 AC=AB,求第三象限内的点 C 的坐标;
(3)如图 3,P 为 y 轴负半轴上一点,过点 P 作 PD⊥PA,且使 PD=PA,过第四象限内的点 D 作 DE⊥x 轴于 E,试判断 OP-DE 的值是否发生变化.若不发生变化,请求其值;若发生变化,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线y=x2-2x-8.
(1)求证:该抛物线与x轴一定有两个交点;
(2)若该抛物线与x轴的两个交点分别为A、B,且它的顶点为P,求△ABP的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】抛物线y=ax2+bx+c(a<0)经过点(-1,0),且满足4a+2b+c>0.以下结论(1)a+b>0;(2)a+c>0;(3)-a+b+c>0;(4)b2-2ac>5a2其中正确的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,一架长25米的梯子,斜靠在竖直的墙上,这时梯子底端离墙7米.
(1)此时梯子顶端离地面多少米?
(2)若梯子顶端下滑4米,那么梯子底端将向左滑动多少米?

查看答案和解析>>
科目: 来源: 题型:
【题目】某区举行“庆祝改革开放40周年”征文比赛,已知每篇参赛征文成绩记![]() 分
分![]() ,组委会从1000篇征文中随机抽取了部分参赛征文,统计了他们的成绩,并绘制了如下不完整的两幅统计图表:
,组委会从1000篇征文中随机抽取了部分参赛征文,统计了他们的成绩,并绘制了如下不完整的两幅统计图表:
征文比赛成绩频数分布表 | ||
分数段 | 频数 | 频率 |
| 38 | 0.38 |
| 0.32 | |
| ||
| 10 | 0.1 |
合计 | 1 | |

请根据以上信息,解决下列问题:
(1)征文比赛成绩频数分布表中![]() 的值是 ;
的值是 ;
(2)补全征文比赛成绩频数分布直方图;
(3)若80分以上(含80分)的征文将被评为一等奖,试估计全市获得一等奖征文的篇数.
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到盈利的过程,下面的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与销售时间t(月)之间的关系(即前t个月的利润总和s与t之间的关系).
根据图象提供的信息,解答下列问题:

(1)由已知图象上的三点坐标,求累积利润s(万元)与时间t(月)之间的函数关系式;
(2)求截止到几月末公司累积利润可达到30万元;
(3)求第8个月公司所获利润为多少万元?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知二次函数![]() 的图象经过点(3,2)。
的图象经过点(3,2)。
(1)求这个二次函数的关系式;
(2)画出它的图象,并指出图象的顶点坐标;
(3)当x>0时,求使y≥2的x的取值范围。
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线![]() 与直线
与直线![]() 相交于
相交于![]() ,
,![]() 两点,且抛物线经过点
两点,且抛物线经过点![]()

(1)求抛物线的解析式.
(2)点![]() 是抛物线上的一个动点(不与点
是抛物线上的一个动点(不与点![]() 点
点![]() 重合),过点
重合),过点![]() 作直线
作直线![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() .当
.当![]() 时,求
时,求![]() 点坐标;
点坐标;
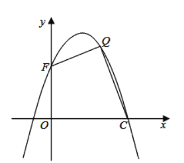
(3)如图所示,设抛物线与![]() 轴交于点
轴交于点![]() ,在抛物线的第一象限内,是否存在一点
,在抛物线的第一象限内,是否存在一点![]() ,使得四边形
,使得四边形![]() 的面积最大?若存在,请求出点
的面积最大?若存在,请求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com