
科目: 来源: 题型:
【题目】![]() (0,
(0, ![]() )
)![]() .
.
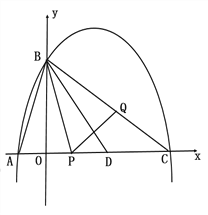
(1)求抛物线的解析式.
(2)抛物线与![]() 轴交于另一个交点为C,点D在线段AC上,已知AD=AB,若动点P从A出发沿线段AC以每秒1个单位长度的速度匀速运动,同时另一个动点Q以某一速度从B出发沿线段BC匀速运动,问是否存在某一时刻,使线段PQ被直线BD垂直平分,若存在,求出点Q的运动速度;若不存在,请说明理由.
轴交于另一个交点为C,点D在线段AC上,已知AD=AB,若动点P从A出发沿线段AC以每秒1个单位长度的速度匀速运动,同时另一个动点Q以某一速度从B出发沿线段BC匀速运动,问是否存在某一时刻,使线段PQ被直线BD垂直平分,若存在,求出点Q的运动速度;若不存在,请说明理由.
(3)在(2)的前提下,过点B的直线![]() 与
与![]() 轴的负半轴交于点M,是否存在点M,使以A、B、M为顶点的三角形与
轴的负半轴交于点M,是否存在点M,使以A、B、M为顶点的三角形与![]() 相似,如果存在,请直接写出M的坐标;若不存在,请说明理由.
相似,如果存在,请直接写出M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
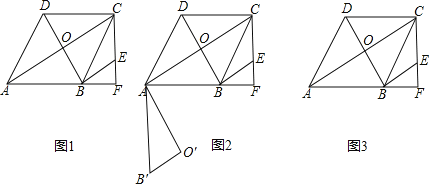
【题目】如图1,在菱形ABCD中,∠DAB=60°,AB=8![]() ,对角线交于点O,CF垂直AB交AB的延长线于点F,过点B作BE∥AC交FC于EF.
,对角线交于点O,CF垂直AB交AB的延长线于点F,过点B作BE∥AC交FC于EF.
(1)求BE的长:
(2)如图2,在OB上有一动点P,将△AOB绕A点顺时针旋转90°至△AOB',P点的对应点为P′,现有一动点Q从P点出发,沿着适当路径先运动到O′点,再沿O′A运动至A点,再从A点沿适当的路径运动至P′点.求Q点的最短运动路径的长;
(3)若△ABO以每秒2![]() 个单位长度的速度沿射线AB向右平移,得到三角形△A1B1O1,当A1与点F重合时停止移动,设运动时间为t,在这个过程中,点O1关于直线BC的对称点为O″,当O″,F,C三点构成的三角形为等腰三角形时,直接写出t的值.
个单位长度的速度沿射线AB向右平移,得到三角形△A1B1O1,当A1与点F重合时停止移动,设运动时间为t,在这个过程中,点O1关于直线BC的对称点为O″,当O″,F,C三点构成的三角形为等腰三角形时,直接写出t的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下列材料,解决问题:
在处理分数和分式问题时,有时由于分子比分母大,或者为了分子的次数告诉于分母的次数,在实际运算时往往难度比较大,这时我们可以将假分数(分式)拆分成一个整数(或整式)与一个真分数的和(或差)的形式,通过对简单式的分析来解决问题,我们称为分离整数法,此法在处理分式或整除问题时颇为有效,现举例说明.
材料1:将分式![]() 拆分成一个整式与一个分式(分子为整数)的和的形式.
拆分成一个整式与一个分式(分子为整数)的和的形式.
解:![]() 9x+y
9x+y![]()
材料2:将分式![]() 拆分成一个整式与一个分式(分子为整数)的和的形式.
拆分成一个整式与一个分式(分子为整数)的和的形式.
解:由分母x+1,可设x2﹣x+3=(x+1)(x+a)+b
则x2﹣x+3=(x+1)(x+a)+b=x2+ax+x+a+b=x2+(a+1)x+a+b
∵对于任意x上述等式成立.
∴![]() 解得:
解得:![]() .
.
∴![]() x﹣2
x﹣2![]() .
.
这样,分式![]() 就拆分成一个整式x﹣2与一个分式
就拆分成一个整式x﹣2与一个分式![]() 的和的形式.
的和的形式.
(1)将分式![]() 拆分成一个整式与一个分子为整数的分式的和的形式,则结果为 .
拆分成一个整式与一个分子为整数的分式的和的形式,则结果为 .
(2)已知整数x使分式![]() 的值为整数,则满足条件的整数x= ;
的值为整数,则满足条件的整数x= ;
(3)已知一个六位整数![]() 能被33整除,求满足条件的x,y的值.
能被33整除,求满足条件的x,y的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某科技开发公司研制出一种新型产品,每件产品的成本为2400元,销售单价定为3000元.在该产品的试销期间,为了促销,鼓励商家购买该新型产品,公司决定商家一次购买这种新型产品不超过10件时,每件按3000元销售;若一次购买该种产品超过10件时,每多购买一件,所购买的全部产品的销售单价均降低10元,但销售单价均不低于2600元.
(1)商家一次购买这种产品多少件时,销售单价恰好为2600元?
(2)设商家一次购买这种产品x件,开发公司所获的利润为y元,求y(元)与x(件)之间的函数关系式,并写出自变量x的取值范围.
(3)该公司的销售人员发现:当商家一次购买产品的件数超过某一数量时,会出现随着一次购买的数量的增多,公司所获的利润反而减少这一情况.为使商家一次购买的数量越多,公司所获的利润最大,公司应将最低销售单价调整为多少元(其它销售条件不变)?
查看答案和解析>>
科目: 来源: 题型:
【题目】高科技发展公司投资500万元,成功研制出一种市场需求量较大的高科技替代产品,并投入资金1500万元作为固定投资,已知生产每件产品的成本是40元.在销售过程中发现:当销售单价定为100元时,年销售量为20万件;销售单价每增加10元,年销售量将减少1万件,设销售单价为x(元),年销售量为y(万件),年获利(年获利=年销售额一生产成本—投资)为z(万元).
(1)试写出y与x之间的函数关系式(不写x的取值范围);
(2)试写出z与x之间的函数关系式(不写x的取值范围);
(3)公司计划,在第一年按年获利最大确定销售单价进行销售;到第二年年底获利不低于1130万元,请借助函数的大致图象说明:第二年的销售单价x(元)应确定在什么范围内?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,∠B=90°,AB=12,BC=24,动点P从点A开始沿边AB向终点B以每秒2个单位长度的速度移动,动点Q从点B开始沿边BC以每秒4个单位长度的速度向终点C移动,如果点P、Q分别从点A、B同时出发,那么△PBQ的面积S随出发时间t(s)如何变化?写出函数关系式及t的取值范围.

查看答案和解析>>
科目: 来源: 题型:
【题目】一水果店主分两批购进同一种水果,第一批所用资金为2400元,因天气原因,水果涨价,第二批所用资金是2700元,但由于第二批单价比第一批单价每箱多10元,以致购买的数量比第一批少25%.
(1)该水果店主购进第一批这种水果每箱的单价是多少元?
(2)该水果店主计划两批水果的售价均定为每千克4元,每箱10千克,实际销售时按计划无损耗售完第一批后,发现第二批水果品质不如第一批,于是该店主将售价下降a%销售,结果还是出现了2%的损耗,但这两批水果销售完后仍赚了不低于2346元,求a的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】 已知在平面直角坐标系xoy中,二次函数y=-2x+bx+c的图像经过点A(-3,0)和点B(0,6)。(1)求此二次函数的解析式;(2)将这个二次函数的图像向右平移5个单位后的顶点设为C,直线BC与x轴相交于点D,求∠sin∠ABD;(3)在第(2)小题的条件下,连接OC,试探究直线AB与OC的位置关系,并且说明理由。
查看答案和解析>>
科目: 来源: 题型:
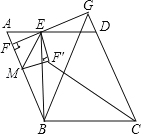
【题目】如图,平行四边形ABCD中,过点B作BE⊥AD于点E,过点E作EF⊥AB于点F,与CD的延长线交于点G,连接BG,且BE=BC,BG=5![]() ,∠BGF=45°,EG=3,若点M是线段BF上的一个动点,将△MEF沿ME所在直线翻折得到△MEF′,连接CF′,则CF′长度的最小值是_____.
,∠BGF=45°,EG=3,若点M是线段BF上的一个动点,将△MEF沿ME所在直线翻折得到△MEF′,连接CF′,则CF′长度的最小值是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com