
科目: 来源: 题型:
【题目】某中学全体同学参加了“关怀贫困学生”爱心捐款活动,该校随机抽查了七、八、九三个年级部分学生捐款情况,将结果绘制成两幅不完整的统计图.根据图中的信息,解决下列问题:
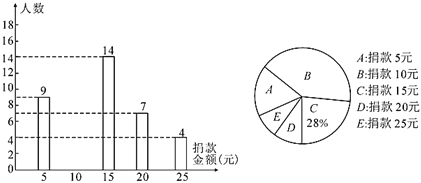
(1)这次共抽查了_______名学生进行统计,其中![]() 类所对应扇形的圆心角的度数为________;
类所对应扇形的圆心角的度数为________;
(2)将条形统计图补充完整;
(3)该校有![]() 名学生,估计该校捐款
名学生,估计该校捐款![]() 元的学生有多少人?
元的学生有多少人?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,一张半径为![]() 的圆形纸片,点
的圆形纸片,点![]() 为圆心,将该圆形纸片沿直线
为圆心,将该圆形纸片沿直线![]() 折叠,直线
折叠,直线![]() 交
交![]() 于
于![]() 两点.
两点.
(1)若折叠后的圆弧恰好经过点![]() ,利用直尺和圆规在图中作出满足条件的一条直线
,利用直尺和圆规在图中作出满足条件的一条直线![]() (不写作法,保留作图痕迹),并求此时线段
(不写作法,保留作图痕迹),并求此时线段![]() 的长度.
的长度.
(2)已知![]() 是
是![]() 一点,
一点,![]() .
.
①若折叠后的圆弧经过点![]() ,则线段
,则线段![]() 长度的取值范围是________.
长度的取值范围是________.
②若折叠后的圆弧与直线![]() 相切于点
相切于点![]() ,则线段
,则线段![]() 的长度为_________
的长度为_________![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】某企业销售某商品,以“线上”与“线下”相结合的方式一共销售了100件.设该商品线下的销售量为![]() 件,线下销售的每件利润为
件,线下销售的每件利润为![]() 元,线上销售的每件利润为
元,线上销售的每件利润为![]() 元.下图中折线
元.下图中折线![]() 、线段
、线段![]() 分别表示
分别表示![]() 与
与![]() 之间的函数关系.
之间的函数关系.
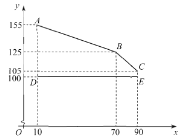
(1)当![]() 时,线上的销售量为_______件;
时,线上的销售量为_______件;
(2)求线段![]() 所表示的
所表示的![]() 与
与![]() 之间的函数表达式;
之间的函数表达式;
(3)当线下的销售量为多少时,售完这100件商品所获得的总利润最大?最大利润是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,以
,以![]() 为直径的
为直径的![]() 交边
交边![]() 于点
于点![]() (点
(点![]() 不与点
不与点![]() 重合),交边
重合),交边![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() .
.
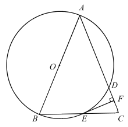
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() .
.
①求![]() 的半径;
的半径;
②连接![]() 交
交![]() 于点
于点![]() ,则
,则![]() _____.
_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知二次函数![]() (
(![]() 为常数).
为常数).
(1)求证:不论![]() 为何值,该二次函数的图像与
为何值,该二次函数的图像与![]() 轴总有公共点.
轴总有公共点.
(2)求证:不论![]() 为何值,该二次函数的图像的顶点都在函数
为何值,该二次函数的图像的顶点都在函数![]() 的图像上.
的图像上.
(3)已知点![]() 、
、![]() ,线段
,线段![]() 与函数
与函数![]() 的图像有公共点,则
的图像有公共点,则![]() 的取值范围是__________.
的取值范围是__________.
查看答案和解析>>
科目: 来源: 题型:
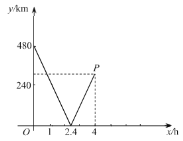
【题目】甲、乙两地之间有一条笔直的公路,快车和慢车分别从甲、乙两地同时出发,沿这条公路匀速相向而行,快车到达乙地后停止行驶,慢车到达甲地后停止行驶,已知快车速度为![]() .下图为两车之间的距离
.下图为两车之间的距离![]() 与慢车行驶时间
与慢车行驶时间![]() 的部分函数图像.
的部分函数图像.
(1)甲、乙两地之间的距离是______km;
(2)点![]() 的坐标为(4,____),解释点
的坐标为(4,____),解释点![]() 的实际意义.
的实际意义.
(3)根据题意,补全函数图像(标明必要的数据).
查看答案和解析>>
科目: 来源: 题型:
【题目】一只不透明的袋子中装有分别标注数字为1,2、3的三个小球,这些球除标注的数字外都相同.
(1)搅匀后从中任意摸出一个球,标注的数字恰好为2的概率是________;
(2)搅匀后从中任意摸出一个球,记录下数字后放回袋中并搅匀,再从袋中任意摸出一个球,求两次数字的和大于3的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】甲乙两人在相同条件下完成了10次射击训练,两人的成绩如图所示。

根据以上信息,整理分析数据如下:
平均成绩/环 | 中位数/环 | 方差/环 | |
甲 | ______ | 7 | 1.2 |
乙 | 7 | ______ | ______ |
(1)完成表格;
(2)根据训练成绩,你认为选派哪一名队员参赛更好?为什么?
查看答案和解析>>
科目: 来源: 题型:
【题目】在四边形 ABCD 中,E 为 BC 边中点.
(Ⅰ)已知:如图,若 AE 平分∠BAD,∠AED=90°,点 F 为 AD 上一点,AF=AB.求证:(1)△ABE≌AFE;(2)AD=AB+CD

(Ⅱ)已知:如图,若 AE 平分∠BAD,DE 平分∠ADC,∠AED=120°,点 F,G 均为 AD上的点,AF=AB,GD=CD.求证:(1)△GEF 为等边三角形;(2)AD=AB+ ![]() BC+CD.
BC+CD.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com