
科目: 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(-1,0),对称轴为直线x=2,下列结论:①abc>0;②9a+c>3b;③4a+b=0;④当x>-1时,y的值随x值的增大而增大.其中正确的结论有( )
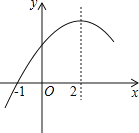
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目: 来源: 题型:
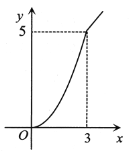
【题目】如图,抛物线![]() 经过点
经过点![]() ,且对称轴为直线
,且对称轴为直线![]() .有四个结论:①
.有四个结论:①![]() ;②
;②![]() ;③
;③![]() ;④若
;④若![]() ,则
,则![]() 时的函数值小于
时的函数值小于![]() 时的函数值.其中正确的结论是( )
时的函数值.其中正确的结论是( )
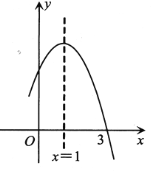
A. ①②B. ②③C. ①④D. ③④
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线![]() 的图象与
的图象与![]() 轴交于
轴交于![]() ,
,![]() 两点,动点
两点,动点![]() 从点
从点![]() 出发,以每秒2个单位长度的速度沿
出发,以每秒2个单位长度的速度沿![]() 方向运动,以
方向运动,以![]() 为边作矩形
为边作矩形![]() (点
(点![]() 在
在![]() 轴上),设运动的时间为
轴上),设运动的时间为![]() 秒.
秒.
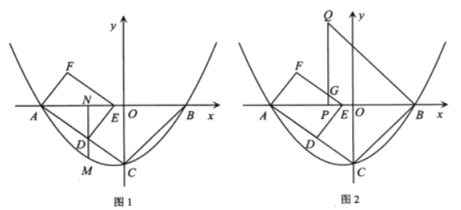
(1)求抛物线![]() 的表达式;
的表达式;
(2)过点![]() 作
作![]() 轴于点
轴于点![]() ,交抛物线于点
,交抛物线于点![]() ,当
,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(3)如图,动点![]() 同时从点
同时从点![]() 出发,以每秒3个单位长度的速度沿
出发,以每秒3个单位长度的速度沿![]() 方向运动,以
方向运动,以![]() 为边作等腰直角三角形
为边作等腰直角三角形![]() ,
,![]() 与
与![]() 交于点
交于点![]() .给出如下定义:在四边形
.给出如下定义:在四边形![]() 中,
中,![]() ,
,![]() 且
且![]() ,我们把这种两组邻边分别相等的四边形叫做“筝形”.当矩形
,我们把这种两组邻边分别相等的四边形叫做“筝形”.当矩形![]() 和等腰三角形
和等腰三角形![]() 重叠的四边形是“筝形”时,求“筝形”的面积.
重叠的四边形是“筝形”时,求“筝形”的面积.
查看答案和解析>>
科目: 来源: 题型:
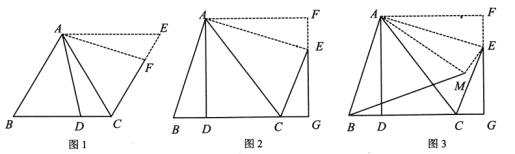
【题目】(探索发现)
如图,![]() 是等边三角形,点
是等边三角形,点![]() 为
为![]() 边上一个动点,将
边上一个动点,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,连接
,连接![]() .小明在探索这个问题时发现四边形
.小明在探索这个问题时发现四边形![]() 是菱形.
是菱形.
小明是这样想的:
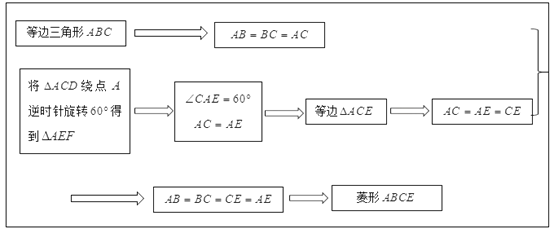
(1)请参考小明的思路写出证明过程;
(2)直接写出线段![]() ,
,![]() ,
,![]() 之间的数量关系:______________;
之间的数量关系:______________;
(理解运用)
如图,在![]() 中,
中,![]() 于点
于点![]() .将
.将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,延长
,延长![]() 与
与![]() ,交于点
,交于点![]() .
.
(3)判断四边形![]() 的形状,并说明理由;
的形状,并说明理由;
(拓展迁移)
(4)在(3)的前提下,如图,将![]() 沿
沿![]() 折叠得到
折叠得到![]() ,连接
,连接![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】“重整行装再出发,驰而不息再争创”,2018年5月8日兰州市召开了新一轮全国文明城市创建启动大会.某校为了更好地贯彻落实创建全国文明城市目标,举办了“我是创城小主人”的知识竞赛.该校七年级、八年级分别有300人,现从中各随机抽取10名同学的测试成绩进行调查分析,成绩如下:
七年级 | 85 | 65 | 84 | 78 | 100 | 78 | 85 | 85 | 98 | 83 |
八年级 | 96 | 60 | 87 | 78 | 87 | 87 | 89 | 100 | 83 | 96 |
整理、描述数据:
分数段 |
|
|
|
|
七年级人数 | 1 | 2 | 5 | 2 |
八年级人数 | 1 | 1 | 5 | 3 |
分析数据:
年级 | 平均数 | 中位数 | 众数 |
七 | 84.1 | _______ | 85 |
八 | 86.3 | 87 | ______ |
得出结论:
(1)根据上述数据,将表格补充完整;
(2)估计该校七、八两个年级学生在本次测试成绩中可以取得优秀的人数![]() 共有多少人?
共有多少人?
(3)你认为哪个年级知识掌握的总体水平较好,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】2019年春节期间,兰州市开展了以“精致兰州志愿同行”为主题的系列志愿服务活动.金老师和程老师积极参加志愿者活动,当时有下列四个志愿者工作岗位供他们选择:
①“送温暖”活动岗位:为困难家庭打扫卫生,为留守儿童提供学业辅导;(分别用![]() ,
,![]() 表示)
表示)
②“送平安”活动岗位:消防安全常识宣传,人员密集场所维护秩序.(分别用![]() ,
,![]() 表示)
表示)
(1)金老师从四个岗位中随机选取一个报名,恰好选择“送温暖”活动岗位的概率是多少?
(2)若金老师和程老师各随机从四个活动岗位中选一个报名,请用树状图或列表法求出他们恰好都选择同一个岗位的概率.
查看答案和解析>>
科目: 来源: 题型:
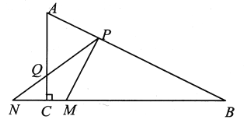
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,动点
,动点![]() ,
,![]() 同时从点
同时从点![]() 出发,分别沿射线
出发,分别沿射线![]() ,
,![]() 方向运动,且满足
方向运动,且满足![]() ,过点
,过点![]() 作
作![]() ,交直线
,交直线![]() 于点
于点![]() ,
,![]() 与直线
与直线![]() 交于点
交于点![]() .设
.设![]() ,
,![]() 的面积为
的面积为![]() ,则
,则![]() 与
与![]() 之间的函数图象大致是( )
之间的函数图象大致是( )
A. 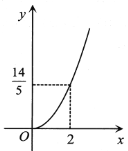 B.
B. 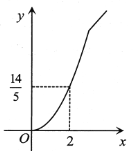 C.
C. 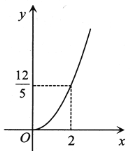
查看答案和解析>>
科目: 来源: 题型:
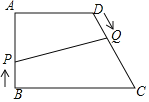
【题目】已知:如图,在四边形ABCD中,AD∥BC,∠A=90°,AB=AD=8cm,CD=10cm,点P从点B出发,沿BA方向匀速运动,速度为1cm/s;同时,点Q从点D出发,沿DC方向匀速运动,速度为lcm/s.连接PQ,设运动时间为t(s)(0<t<8).解答下列问题:
(1)当t为何值时,PQ∥AD?
(2)设四边形APQD的面积为y(cm2),求y与t的函数关系式;
(3)是否存在某一时刻t,使S四边形APQO:S四边形BCQP=17:27?若存在,求出t的值,并求此时PQ的长;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】(问题)如图①,在a×b×c(长×宽×高,其中a,b,c为正整数)个小立方块组成的长方体中,长方体的个数是多少?
(探究)

探究一:
(1)如图②,在2×1×1个小立方块组成的长方体中,棱AB上共有1+2=![]() =3条线段,棱AC,AD上分别只有1条线段,则图中长方体的个数为3×1×1=3.
=3条线段,棱AC,AD上分别只有1条线段,则图中长方体的个数为3×1×1=3.
(2)如图③,在3×1×1个小立方块组成的长方体中,棱AB上共有1+2+3=![]() =6条线段,棱AC,AD上分别只有1条线段,则图中长方体的个数为6×1×1=6.
=6条线段,棱AC,AD上分别只有1条线段,则图中长方体的个数为6×1×1=6.
(3)依此类推,如图④,在a×1×1个小立方块组成的长方体中,棱AB上共有1+2+…+a=![]() 线段,棱AC,AD上分别只有1条线段,则图中长方体的个数为______.
线段,棱AC,AD上分别只有1条线段,则图中长方体的个数为______.
探究二:
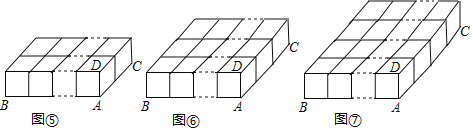
(4)如图⑤,在a×2×1个小立方块组成的长方体中,棱AB上有![]() 条线段,棱AC上有1+2=
条线段,棱AC上有1+2=![]() =3条线段,棱AD上只有1条线段,则图中长方体的个数为
=3条线段,棱AD上只有1条线段,则图中长方体的个数为![]() ×3×1=
×3×1=![]() .
.
(5)如图⑥,在a×3×1个小立方块组成的长方体中,棱AB上有![]() 条线段,棱AC上有1+2+3=
条线段,棱AC上有1+2+3=![]() =6条线段,棱AD上只有1条线段,则图中长方体的个数为______.
=6条线段,棱AD上只有1条线段,则图中长方体的个数为______.
(6)依此类推,如图⑦,在a×b×1个小立方块组成的长方体中,长方体的个数为______.
探究三:
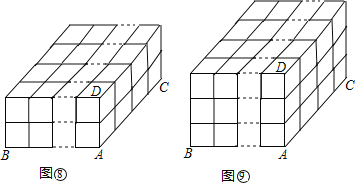
(7)如图⑧,在以a×b×2个小立方块组成的长方体中,棱AB上有![]() 条线段,棱AC上有
条线段,棱AC上有![]()
条线段,棱AD上有1+2=![]() =3条线段,则图中长方体的个数为
=3条线段,则图中长方体的个数为![]() ×
×![]() ×3=
×3=![]() .
.
(8)如图⑨,在a×b×3个小立方块组成的长方体中,棱AB上有![]() 条线段,棱AC上有
条线段,棱AC上有![]() 条线段,棱AD上有1+2+3=
条线段,棱AD上有1+2+3=![]() =6条线段,则图中长方体的个数为______.
=6条线段,则图中长方体的个数为______.
(结论)如图①,在a×b×c个小立方块组成的长方体中,长方体的个数为______.
(应用)在2×3×4个小立方块组成的长方体中,长方体的个数为______.
(拓展)
如果在若干个小立方块组成的正方体中共有1000个长方体,那么组成这个正方体的小立方块的个数是多少?请通过计算说明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com