
科目: 来源: 题型:
【题目】阅读下面材料:
上课时孙老师提出这样一个问题:对于任意实数![]() ,关于
,关于![]() 的不等式
的不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
小明的思路是:原不等式等价于![]() ,设函数
,设函数![]() ,
,![]() ,画出两个函数的图象的示意图,于是原问题转化为函数
,画出两个函数的图象的示意图,于是原问题转化为函数![]() 的图象在
的图象在![]() 的图象上方时
的图象上方时![]() 的取值范围.
的取值范围.

请结合小明的思路回答:
对于任意实数![]() ,关于
,关于![]() 的不等式
的不等式![]() 恒成立,则
恒成立,则![]() 的取值范围是_____.
的取值范围是_____.
参考小明思考问题的方法,解决问题:
关于![]() 的方程
的方程![]() 在
在![]() 范围内有两个解,求
范围内有两个解,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四边形![]() 内接于
内接于![]() ,对角线
,对角线![]() 为
为![]() 的直径,过点
的直径,过点![]() 作AC的垂线交AD的延长线于点E,点F为CE的中点,连接DB,DC,DF.
作AC的垂线交AD的延长线于点E,点F为CE的中点,连接DB,DC,DF.
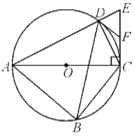
(1)求证:DF是![]() 的切线;
的切线;
(2)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,A(-4,3),B(0,1),将线段AB沿
中,A(-4,3),B(0,1),将线段AB沿![]() 轴的正方向平移
轴的正方向平移![]() 个单位,得到线段A′B′,且A′,B′恰好都落在反比例函数
个单位,得到线段A′B′,且A′,B′恰好都落在反比例函数![]() 的图象上.
的图象上.
(1)用含![]() 的代数式表示点A′,B′的坐标;
的代数式表示点A′,B′的坐标;
(2)求![]() 的值和反比例函数
的值和反比例函数![]() 的表达式;
的表达式;
(3)点![]() 为反比例函数
为反比例函数![]() 图象上的一个动点,直线
图象上的一个动点,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,请直接写出点C的坐标.
,请直接写出点C的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】中华文明,源远流长;中华汉字,寓意深广.为了传承优秀传统文化,某校团委组织了一次全校1000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了200名学生的成绩(成绩![]() 取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
成绩 | 频数 | 频率 |
| 10 | 0.05 |
| 20 | 0.10 |
| 30 |
|
|
| 0.30 |
| 80 | 0.40 |
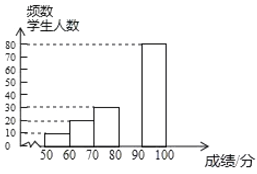
请根据所给的信息,解答下列问题:
(1)![]() _____,
_____,![]() _____;
_____;
(2)请补全频数分布直方图;
(3)这次比赛成绩的中位数会落在______分数段;
(4)若成绩在90分以上(包括90分)的为优等,则该校参加这次比赛的1000名学生中成绩优等的大约有多少人?
查看答案和解析>>
科目: 来源: 题型:
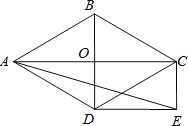
【题目】如图,菱形ABCD的对角线AC和BD交于点O,分别过点C. D作CE∥BD,DE∥AC,CE和DE交于点E.
(1)求证:四边形ODEC是矩形;
(2)当∠ADB=60°,AD=2![]() 时,求EA的长。
时,求EA的长。
查看答案和解析>>
科目: 来源: 题型:
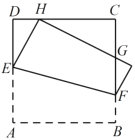
【题目】如图,将正方形![]() 折叠,使顶点
折叠,使顶点![]() 与
与![]() 边上的一点
边上的一点![]() 重合(
重合(![]() 不与端点
不与端点![]() ,
,![]() 重合),折痕交
重合),折痕交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,边
,边![]() 折叠后与边
折叠后与边![]() 交于点
交于点![]() ,设正方形
,设正方形![]() 的周长为
的周长为![]() ,
,![]() 的周长为
的周长为![]() ,则
,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.2
D.2
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线![]() 交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个结论:
交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个结论:
①点C的坐标为(0,m);
②当m=0时,△ABD是等腰直角三角形;
③若a=-1,则b=4;
④抛物线上有两点P(![]() ,
,![]() )和Q(
)和Q(![]() ,
,![]() ),若
),若![]() <1<
<1<![]() ,且
,且![]() +
+![]() >2,则
>2,则![]() >
>![]() .
.
其中结论正确的序号是( )

A.①②B.①②③C.①②④D.②③④
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,等腰![]() 的底边
的底边![]() 在
在![]() 轴上,已知
轴上,已知![]() ,抛物线
,抛物线![]() (其中
(其中![]() )经过
)经过![]() 三点,双曲线
三点,双曲线![]() (其中
(其中![]() )经过点
)经过点![]() 轴,
轴,![]() 轴,垂足分别为
轴,垂足分别为![]() 且
且![]()
(1)求出![]() 的值;当
的值;当![]() 为直角三角形时,请求出
为直角三角形时,请求出![]() 的表达式;
的表达式;
(2)当![]() 为正三角形时,直线
为正三角形时,直线![]() 平分
平分![]() ,求
,求![]() 时
时![]() 的取值范围;
的取值范围;
(3)抛物线![]() (其中
(其中![]() )有一时刻恰好经过
)有一时刻恰好经过![]() 点,且此时抛物线与双曲线
点,且此时抛物线与双曲线![]() (其中
(其中![]() )有且只有一个公共点
)有且只有一个公共点![]() (其中
(其中![]() ),我们不妨把此时刻的
),我们不妨把此时刻的![]() 记作
记作![]() ,请直接写出抛物线
,请直接写出抛物线![]() (其中
(其中![]() )与双曲线
)与双曲线![]() (其中
(其中![]() )有一个公共点时
)有一个公共点时![]() 的取值范围.(
的取值范围.(![]() 是已知数)
是已知数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com