
科目: 来源: 题型:
【题目】长春的冬天经常下雪,为了提高清雪的效率,市政府启用了清雪机,已知一台清雪机的工作效率相当于一名环卫工人的200倍,若用这台清雪机清理9000立方米的积雪,要比150名环卫工人清理这些积雪少用2小时,求一台清雪机每小时清雪多少立方米?
查看答案和解析>>
科目: 来源: 题型:
【题目】综合与探究:
如图1,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),顶点为
的左侧),顶点为![]() ,
,![]() 为对称轴右侧抛物线的一个动点,直线
为对称轴右侧抛物线的一个动点,直线![]() 与
与![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 轴于点
轴于点![]() .
.
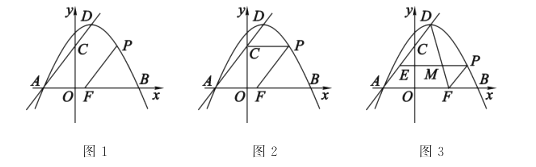
(1)求直线![]() 的函数表达式及点
的函数表达式及点![]() 的坐标;
的坐标;
(2)如图2,当![]() 轴时,将
轴时,将![]() 以每秒1个单位长度的速度沿
以每秒1个单位长度的速度沿![]() 轴的正方向平移,当点
轴的正方向平移,当点![]() 与点
与点![]() 重合时停止平移.设平移
重合时停止平移.设平移![]() 秒时,在平移过程中
秒时,在平移过程中![]() 与四边形
与四边形![]() 重叠部分的面积为
重叠部分的面积为![]() ,求
,求![]() 关于
关于![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(3)如图3,过点![]() 作
作![]() 轴的平行线,交直线
轴的平行线,交直线![]() 于点
于点![]() ,直线
,直线![]() 与
与![]() 交于点
交于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() .
.
①当![]() 时,求
时,求![]() 的值;
的值;
②试探究点![]() 在运动过程中,是否存在值
在运动过程中,是否存在值![]() ,使四边形
,使四边形![]() 是菱形?若存在,请直接写出点
是菱形?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】综合与实践:
动手操作:如图1,四边形![]() 是一张矩形纸片,
是一张矩形纸片,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 边上,且
边上,且![]() ,连接
,连接![]() ,
,![]() .将
.将![]() ,
,![]() 分别沿
分别沿![]() ,
,![]() 折叠,点
折叠,点![]() ,
,![]() 分别落在点
分别落在点![]() ,
,![]() 处.
处.
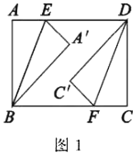
探究展示:
(1)“刻苦小组”发现:![]() ,且
,且![]() ,并展示了如下的证明过程.
,并展示了如下的证明过程.
证明:在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
又∵![]() ,
,
∴![]() .
.
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() .(依据1)
.(依据1)
∴![]() .
.
∴![]() .(依据2)
.(依据2)
反思交流:①上述证明过程中的“依据1”与“依据2”分别指什么?
②“勤奋小组”认为:还可以通过证明四边形![]() 是平行四边形获证,请你根据“勤奋小组”的证明思路写出证明过程.
是平行四边形获证,请你根据“勤奋小组”的证明思路写出证明过程.
猜想证明:
(2)如图2,折叠过程中,当点![]() ,
,![]() 在直线
在直线![]() 的同侧时,延长
的同侧时,延长![]() 交
交![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,则四边形
,则四边形![]() 是什么特殊四边形?请说明理由.
是什么特殊四边形?请说明理由.
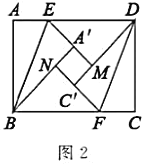
联想拓广:
(3)如图3,连接![]() ,
,![]() ,
,![]() .
.

①当![]() 时,
时,![]() 的长为________;
的长为________;
②![]() 的长有最大值吗?若有,请你直接写出
的长有最大值吗?若有,请你直接写出![]() 长的最大值和此时四边形
长的最大值和此时四边形![]() 的形状;若没有,请说明理由.
的形状;若没有,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】请阅读以下材料,并完成相应任务:
斐波那契(约1170-1250)是意大利数学家.1202年,撰写了《算盘书》一书,他是第一个研究了印度和阿拉伯数学理论的欧洲人,他还曾在埃及、叙利亚、希腊,以及意大利西西里和法国普罗旺斯等地研究数学.他研究了一列非常奇妙的数:0,1,1,2,3,5,8,13,21,34,55,89,144……这列数,被称为斐波那契数列.其特点是从第3项开始,每一项都等于前两项之和,斐波那契数列还有很多有趣的性质,在实际生活中也有广泛的应用.

任务:(1)填写下表并写出通过填表你发现的规律:
项 | 第2项 | 第3项 | 第4项 | 第5项 | 第6项 | 第7项 | 第8项 | 第9项 | … |
这一项的平方 | 1 | 1 | 4 | 9 | 25 | ________ | _______ | 441 | … |
这一项的前、后两项的积 | 0 | 2 | 3 | 10 | 24 | _______ | _______ | 442 | … |
规律:_____________;
(2)现有长为![]() 的铁丝,要截成
的铁丝,要截成![]() 小段,每段的长度不小于
小段,每段的长度不小于![]() ,如果其中任意三小段都不能拼成三角形,则
,如果其中任意三小段都不能拼成三角形,则![]() 的最大值为___________________.
的最大值为___________________.
查看答案和解析>>
科目: 来源: 题型:
【题目】为全面推进“三供一业”分离移交工作,甲、乙两个工程队承揽了某社区2400米的电路管道铺设工程.已知甲队每天铺设管道的长度是乙队每天铺设管道长度的1.5倍,若两队各自独立完成1200米的铺设任务,则甲队比乙队少用10天.
(1)求甲、乙两工程队每天分别铺设电路管道多少米;
(2)若甲队参与该项工程的施工时间不得超过20天,则乙队至少施工多少天才能完成该项工程?
查看答案和解析>>
科目: 来源: 题型:
【题目】在新中国成立70周年之际,某校开展了“校园文化艺术”活动,活动项目有:书法、绘画、声乐和器乐,要求全校学生人人参加,并且每人只能参加其中一项活动,政教处在该校学生中随机抽取了100名学生进行调查和统计,并绘制了如下两幅不完整的统计图,请结合图中相关数据解答下列问题:
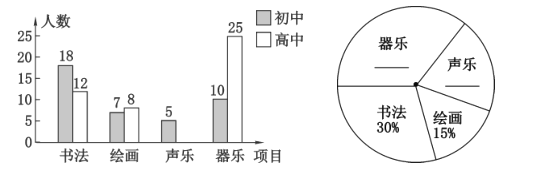
(1)请补全条形统计图和扇形统计图;
(2)该校初中学生中,参加“书法”项目的学生所占的百分比是多少?
(3)若该校共有1500人,请估计其中参加“器乐”项目的高中学生有多少人?
(4)经政教处对所有参加“绘画”项目的作品进行评比,共选出2名初中学生和2名高中学生的最佳作品,学校决定从这4名学生中随机抽取2人作为学生会“绘画社团”的团生,那么正好抽到一名初中学生和一名高中学生的概率是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知反比例函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象在第一象限交于
的图象在第一象限交于![]() 两点,一次函数的图象与
两点,一次函数的图象与![]() 轴交于点
轴交于点![]() .
.
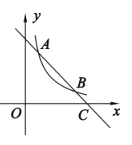
(1)求反比例函数和一次函数的表达式;
(2)当![]() 为何值时,
为何值时,![]() ?
?
(3)已知点![]() ,过点
,过点![]() 作
作![]() 轴的平行线,在第一象限内交一次函数
轴的平行线,在第一象限内交一次函数![]() 的图象于点
的图象于点![]() ,交反比例函数
,交反比例函数![]() 的图象于点
的图象于点![]() .结合函数图象直接写出当
.结合函数图象直接写出当![]() 时
时![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校为了解学生“阳光体育运动”的实施情况,随机调查了40名学生一周的体育锻炼时间,并绘制成了如下图所示的条形统计图,根据统计图提供的数据,该校40名同学一周参加体育锻炼时间的众数与中位数分别是( )
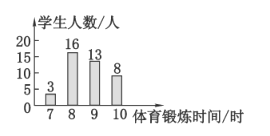
A.8,9B.8,8C.9,8D.10,9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com