
科目: 来源: 题型:
【题目】学校为了解全校2000名学生到校上学的方式,在全校随机抽取了若干名学生进行问卷调查.问卷给出了五种上学方式供学生选择,每人只能选一项,且不能不选,将调查得到的结果绘制成如图所示的统计图和频数表(均不完整).
到校方式 | 频数 | 频率 |
自行车 | 24 | 0.3 |
步行 | ||
公交车 | 0.325 | |
私家车 | 10 | |
其他 | 4 |
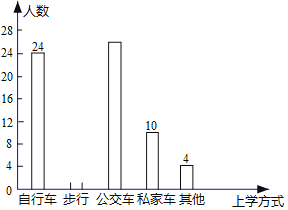
由图表中给出的信息回答下列问题:
(1)问:在这次调查中,一共抽取了多少名学生?
(2)补全频数分布直方图.
(3)估计全校所有学生中有多少人步行上学.
查看答案和解析>>
科目: 来源: 题型:
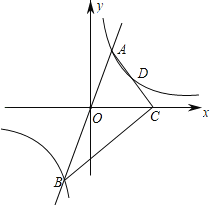
【题目】如图,在平面直角坐标系中,菱形OABC的边长为2,∠AOC=60°,点D为AB边上的一点,经过O,A,D三点的抛物线与x轴的正半轴交于点E,连结AE交BC于点F,当DF⊥AB时,CE的长为__.
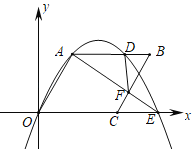
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,某轮船以每小时30海里的速度向正东方向航行,上午8:00,测得小岛C在轮船A的北偏东45°方向上;上午10:00,测得小岛C在轮船B的北偏西30°方向上,则轮船在航行中离小岛最近的距离约为__海里(精确到1海里,参考数据![]() ≈1.414,
≈1.414,![]() ≈1.732).
≈1.732).
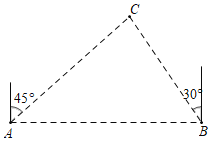
查看答案和解析>>
科目: 来源: 题型:
【题目】有一个著名的希波克拉蒂月牙问题:如图1,以直角三角形的各边为直径分别向上作半圆,则直角三角形的面积可表示成两个月牙形的面积之和,现将三个半圆纸片沿直角三角形的各边向下翻折得到图2,把较小的两张半圆纸片的重叠部分面积记为S1,大半圆纸片未被覆盖部分的面积记为S2,则直角三角形的面积可表示成( )
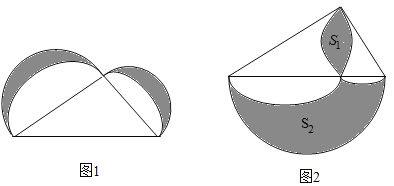
A.S1+S2B.S2﹣S1C.S2﹣2S1D.S1S2
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,过原点的直线与反比例函数y=![]() (k>0)的图象交于点A,B两点,在x轴有一点C(3,0),AC⊥BC,连结AC交反比例函数图象于点D,若AD=CD,则k的值为( )
(k>0)的图象交于点A,B两点,在x轴有一点C(3,0),AC⊥BC,连结AC交反比例函数图象于点D,若AD=CD,则k的值为( )
A.![]() B.2C.2
B.2C.2![]() D.4
D.4
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,抛物线![]() :
:![]() 与直线l:
与直线l:![]() 交于x轴上的一点A,和另一点
交于x轴上的一点A,和另一点![]()
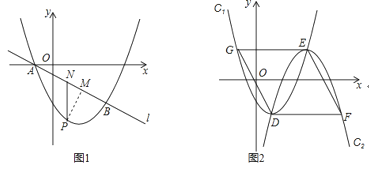
![]() 求抛物线
求抛物线![]() 的解析式;
的解析式;
![]() 点P是抛物线
点P是抛物线![]() 上的一个动点
上的一个动点![]() 点P在A,B两点之间,但不包括A,B两点
点P在A,B两点之间,但不包括A,B两点![]() 于点M,
于点M,![]() 轴交AB于点N,求MN的最大值;
轴交AB于点N,求MN的最大值;
![]() 如图2,将抛物线
如图2,将抛物线![]() 绕顶点旋转
绕顶点旋转![]() 后,再作适当平移得到抛物线
后,再作适当平移得到抛物线![]() ,已知抛物线
,已知抛物线![]() 的顶点E在第一象限的抛物线
的顶点E在第一象限的抛物线![]() 上,且抛持线
上,且抛持线![]() 与抛物线
与抛物线![]() 交于点D,过点D作
交于点D,过点D作![]() 轴交抛物线
轴交抛物线![]() 于点F,过点E作
于点F,过点E作![]() 轴交抛物线
轴交抛物线![]() 于点G,是否存在这样的抛物线
于点G,是否存在这样的抛物线![]() ,使得四边形DFEG为菱形?若存在,请求E点的横坐标;若不存在,请说明理由.
,使得四边形DFEG为菱形?若存在,请求E点的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AB是⊙O的直径,且AB=6.点C是⊙O上的一动点,连接AC,BC,在AC的延长线上取一点D,使得∠CBD=∠DAB,点G为DB的中点,点E为BG的中点,连接AE交BC于点F.
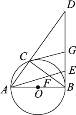
(1)试判断直线BD与⊙O的位置关系,并说明理由;
(2)当∠CGB=60°时,求![]() 的长;
的长;
(3)当AE∥CG时,连接GF,若AF=4,求BD的长.
查看答案和解析>>
科目: 来源: 题型:
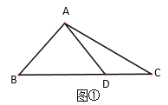
【题目】(问题探究)课堂上老师提出了这样的问题:“如图①,在![]() 中,
中,![]() ,点
,点![]() 是
是![]() 边上的一点,
边上的一点,![]() ,求
,求![]() 的长”.某同学做了如下的思考:如图②,过点
的长”.某同学做了如下的思考:如图②,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,进而求解,请回答下列问题:
,进而求解,请回答下列问题:
(1)![]() ___________度;
___________度;
(2)求![]() 的长.
的长.
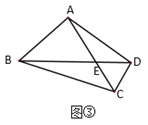
(拓展应用)如图③,在四边形![]() 中,
中,![]() ,对角线
,对角线![]() 相交于点
相交于点![]() ,且
,且![]() ,
,![]() ,则
,则![]() 的长为_____________.
的长为_____________.

查看答案和解析>>
科目: 来源: 题型:
【题目】王妈妈在莲花商场里购买单价总和是90元的商品甲、乙、丙共两次,其中甲的单价是20元,乙的单价是40元,甲商品第一次购买的数量是第二次购买数量的两倍,乙商品第一次购买的数量与丙商品第二次购买的数量相等,两次购买商品甲、乙、丙的数量和总费用如下表:
购买商品甲的 数量(个) | 购买商品乙的 数量(个) | 购买商品丙的 数量(个) | 购买总费用(元) | |
第一次购物 | 4 | 440 | ||
第二次购物 | 7 | 490 |
(1)求两次购买甲、乙、丙三种商品的总数量分别是多少?
(2)由于莲花商场物美价廉,王妈妈打算第三次前往购买商品甲、乙、丙,设三种商品的数量总和为a个,其中购买乙商品数量是甲商品数量的3倍,购买总费用为1 280元,求a的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com