
科目: 来源: 题型:
【题目】已知:如图,∠EOF=60°,在射线OE上取一点A,使OA=10cm,在射线OF上取一点B,使OB=16cm.以OA、OB为邻边作平行四边形OACB.若点P在射线OF上,点Q在线段CA上,且CQ:OP=1:2.设CQ=a(a>0).

(1)连接PQ,当a=2时,求线段PQ的长度.
(2)若以点P、B、C、Q四点为顶点的四边形是平行四边形时,求a的值.
(3)连接PQ,以PQ所在的直线为对称轴,作点C关于直线PQ的对称点C',当点C′恰好落在平行四边形OACB的边上或者边所在的直线上时,直接写出a的值.
查看答案和解析>>
科目: 来源: 题型:
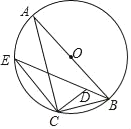
【题目】如图Rt△ABC中,∠ACB=90°,⊙O是△ABC的外接圆,E为⊙O上一点,连结CE,过C作CD⊥CE,交BE于点D,已知![]() ,则tan∠ACE=_____.
,则tan∠ACE=_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,AB=AC=10,点D是BC边上的一动点(不与B、C重合),∠ADE=∠B=∠α,DE交AB于点E,且tan∠α=0.75,有以下的结论:
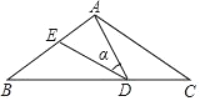
①△DBE∽△ACD;②△ADE∽△ACD;③△BDE为直角三角形时,BD为8或3.5;
④0<BE≤5.其中正确的结论是_______(填入正确结论的序号)
查看答案和解析>>
科目: 来源: 题型:
【题目】一个不透明的袋中装有2个黄球,1个红球和1个白球,除色外都相同.
(1)搅匀后,从袋中随机出一个球,恰好是黄球的概是_____?
(2)搅匀后,从中随机摸出两个球,求摸到一个红球和一个黄球的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是抛物线的顶点.
是抛物线的顶点.
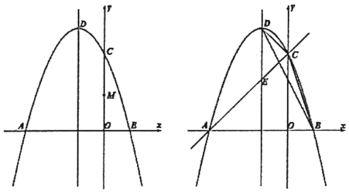
(1)求抛物线的解析式;
(2)点![]() 是
是![]() 轴正半轴上的一点,
轴正半轴上的一点,![]() ,点
,点![]() 在对称轴左侧的抛物线上运动,直线
在对称轴左侧的抛物线上运动,直线![]() 交抛物线的对称轴于点
交抛物线的对称轴于点![]() ,连接
,连接![]() ,当
,当![]() 平分
平分![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(3)直线![]() 交对称轴于点
交对称轴于点![]() ,
,![]() 是坐标平面内一点,当
是坐标平面内一点,当![]() 与
与![]() 全等时,请直接写出点
全等时,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,正方形
,正方形![]() 的边长为2,将正方形
的边长为2,将正方形![]() 绕点
绕点![]() 旋转一周,连接
旋转一周,连接![]() 、
、![]() 、
、![]() .
.
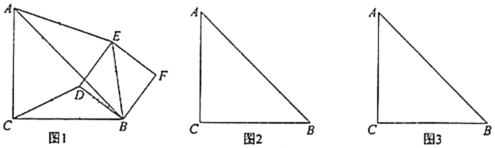
(1)猜想:![]() 的值是__________,直线
的值是__________,直线![]() 与直线
与直线![]() 相交所成的锐角度数是__________;
相交所成的锐角度数是__________;
(2)探究:直线![]() 与
与![]() 垂直时,求线段
垂直时,求线段![]() 的长;
的长;
(3)拓展:取![]() 的中点
的中点![]() ,连接
,连接![]() ,直接写出线段
,直接写出线段![]() 长的取值范围.
长的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】受“新冠”疫情影响,全国中小学延迟开学,很多学校都开展起了“线上教学”,市场上对手写板的需求激增.重庆某厂家准备3月份紧急生产A,B两种型号的手写板,若生产20个A型号和30个B型号手写板,共需要投入36000元;若生产30个A型号和20个B型号手写板,共需要投入34000元.
(1)请问生产A,B两种型号手写板,每个各需要投入多少元的成本?
(2)经测算,生产的A型号手写板每个可获利200元,B型号手写板每个可获利400元,该厂家准备用10万元资金全部生产这两种手写板,总获利w元,设生产了A型号手写板a个,求w关于a的函数关系式;
(3)在(2)的条件下,若要求生产A型号手写板的数量不能少于B型号手写板数量的2倍,请你设计出总获利最大的生产方案,并求出最大总获利.
查看答案和解析>>
科目: 来源: 题型:
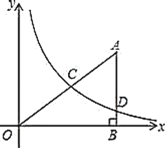
【题目】如图,在平面直角坐标系中,![]() 为坐标原点,
为坐标原点,![]() 的边
的边![]() 垂直
垂直![]() 轴于点
轴于点![]() ,反比例函数
,反比例函数![]()
![]() 的图象经过
的图象经过![]() 的中点
的中点![]() ,与边
,与边![]() 相交于点
相交于点![]() ,
,![]() .
.
(1)求反比例函数![]() 的解析式;
的解析式;
(2)求![]() 的值;
的值;
(3)经过![]() 、
、![]() 两点的直线的解析式是__________.
两点的直线的解析式是__________.
查看答案和解析>>
科目: 来源: 题型:
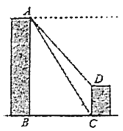
【题目】如图,甲、乙两座建筑物的水平距离![]() 为
为![]() ,从甲的顶部
,从甲的顶部![]() 处测得乙的顶部
处测得乙的顶部![]() 处的俯角为48°,测得底部
处的俯角为48°,测得底部![]() 处的俯角为58°,求乙建筑物
处的俯角为58°,求乙建筑物![]() 的高度.(参考数据:
的高度.(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() .结果取整数)
.结果取整数)
查看答案和解析>>
科目: 来源: 题型:
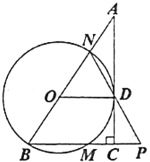
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 在
在![]() 上,以线段
上,以线段![]() 的长为半径的
的长为半径的![]() 与
与![]() 相切于点
相切于点![]() ,
,![]() 分别交
分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,连接
,连接![]() 并延长交
并延长交![]() 延长线于点
延长线于点![]() .
.
(1)求证:![]() ;
;
(2)已知![]() 的半径为5.
的半径为5.
①若![]() ,则
,则![]() __________;
__________;
②连接![]() ,当
,当![]() __________时,四边形
__________时,四边形![]() 是菱形.
是菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com