
科目: 来源: 题型:
【题目】如图,对称轴为直线![]() 的抛物线
的抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() ,与
,与![]() 轴交于
轴交于![]() 点,抛物线顶点为
点,抛物线顶点为![]() ,直线
,直线![]() 交
交![]() 轴于
轴于![]() 点.
点.
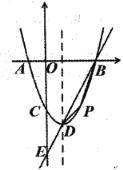
(1)求抛物线函数表达式;
(2)若点![]() 是位于直线
是位于直线![]() 下方抛物线上的一动点,以
下方抛物线上的一动点,以![]() 、
、![]() 为相邻的两边作平行四边形
为相邻的两边作平行四边形![]() ,当平行四边形
,当平行四边形![]() 的面积最大时,求此时平行四边形
的面积最大时,求此时平行四边形![]() 的面积
的面积![]() 及点
及点![]() 的坐标;
的坐标;
(3)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,正方形![]() 中,
中,![]() 为
为![]() 边上任意点,
边上任意点,![]() 平分
平分![]() ,交
,交![]() 于点
于点![]() .
.
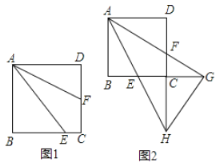
(1)如图1,当点![]() 恰好为
恰好为![]() 中点,延长
中点,延长![]() 交
交![]() 的延长线于点
的延长线于点![]() ,求证:
,求证:![]() ;
;
(2)在(1)的条件下,求证:![]() ;
;
(3)如图2,延长![]() 交
交![]() 的延长线于点
的延长线于点![]() ,延长
,延长![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,当
,当![]() 时,求证:
时,求证:![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】某家具商场计划购进某种餐桌、餐椅进行销售,有关信息如表:
原进价(元/张) | 零售价(元/张) | 成套售价(元/套) | |
餐桌 | a | 270 | 500元 |
餐椅 | a﹣110 | 70 |
已知用600元购进的餐桌数量与用160元购进的餐椅数量相同.
(1)求表中a的值;
(2)若该商场购进餐椅的数量是餐桌数量的5倍还多20张,且餐桌和餐椅的总数量不超过200张.该商场计划将一半的餐桌成套(一张餐桌和四张餐椅配成一套)销售,其余餐桌、餐椅以零售方式销售.请问怎样进货,才能获得最大利润?最大利润是多少?
(3)由于原材料价格上涨,每张餐桌和餐椅的进价都上涨了10元,但销售价格保持不变.商场购进了餐桌和餐椅共200张,应怎样安排成套销售的销售量(至少10套以上),使得实际全部售出后,最大利润与(2)中相同?请求出进货方案和销售方案.
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙、丙三个家电厂家在广告中都声称,他们的某种电子产品在正常情况下的使用寿命都是![]() 年,经质量检测部门对这三家销售的产品的使用寿命进行跟踪调查,统计结果如下:(单位:年)
年,经质量检测部门对这三家销售的产品的使用寿命进行跟踪调查,统计结果如下:(单位:年)
甲厂:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]()
乙厂:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]()
丙厂:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]()
请回答下面问题:
(1)填空:
平均数 | 众数 | 中位数 | |
甲厂 | _____ |
|
|
乙厂 |
| ______ |
|
丙厂 |
|
| ______ |
(2)这三个厂家的销售广告分别利用了哪一种表示集中趋势的特征数;
(3)如果你是顾客,你会买三家中哪一家的电子产品?为什么?
查看答案和解析>>
科目: 来源: 题型:
【题目】在矩形![]() 中,分别以
中,分别以![]() ,
,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 轴,建立如图所示的平面直角坐标系.
轴,建立如图所示的平面直角坐标系.![]() 是
是![]() 边上一个动点(不与
边上一个动点(不与![]() ,
,![]() 重合),过点
重合),过点![]() 的反比例函数
的反比例函数![]()
![]() 的图象与边
的图象与边![]() 交于点
交于点![]() ,已知
,已知![]() ,
,![]() ,将
,将![]() 沿
沿![]() 折叠,点
折叠,点![]() 恰好落在边
恰好落在边![]() 上的点
上的点![]() 处,则
处,则![]() ________.
________.
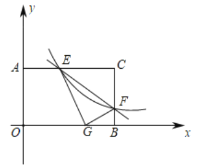
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)如图①,圆![]() 的半径为2,圆内有一点
的半径为2,圆内有一点![]() ,
,![]() ,若弦
,若弦![]() 过点
过点![]() ,则弦
,则弦![]() 长度的最大值为______;最小值为______;
长度的最大值为______;最小值为______;
(2)如图②,将![]() 放在如图所示的平面直角坐标系中,点
放在如图所示的平面直角坐标系中,点![]() 与原点
与原点![]() 重合,点
重合,点![]() 在
在![]() 轴的正半轴上,
轴的正半轴上,![]() ,
,![]() ,
,![]() .在
.在![]() 轴上方是否存在点
轴上方是否存在点![]() ,使得
,使得![]() ,且
,且![]() ?若存在,请求出点
?若存在,请求出点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
(3)如图③,![]() 是李叔叔家的一块空地示意图,其中
是李叔叔家的一块空地示意图,其中![]() ,
,![]() 米,
米,![]() 米.现在他利用周边地的情况,把原来的三角形地拓展成符合条件的面积尽可能大、周长尽可能长的四边形地,用来建鱼塘.若李叔叔想建的鱼塘是四边形
米.现在他利用周边地的情况,把原来的三角形地拓展成符合条件的面积尽可能大、周长尽可能长的四边形地,用来建鱼塘.若李叔叔想建的鱼塘是四边形![]() ,且满足
,且满足![]() ,你认为李叔叔的想法能实现吗?若能,求出这个四边形鱼塘面积和周长的最大值;若不能,请说明理由.
,你认为李叔叔的想法能实现吗?若能,求出这个四边形鱼塘面积和周长的最大值;若不能,请说明理由.
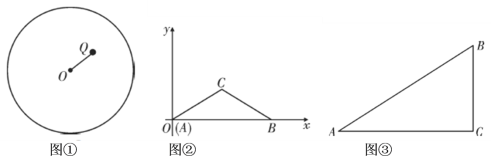
查看答案和解析>>
科目: 来源: 题型:
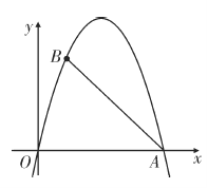
【题目】如图,抛物线![]() 过坐标原点和
过坐标原点和![]() ,
,![]() 两点.
两点.
(1)求该抛物线的表达式;
(2)在线段![]() 右侧的抛物线上是否存在一点
右侧的抛物线上是否存在一点![]() ,使得
,使得![]() 分
分![]() 的面积为
的面积为![]() 两部分?若存在,求出点
两部分?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
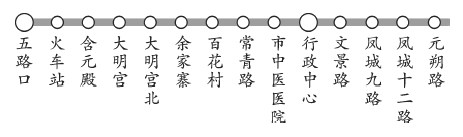
【题目】西安地铁的开通运行给市民的出行方式带来了一些变化,乐乐和小敏利用寒假时间,以问卷的方式对西安市民认为地铁站存在的问题进行调查,如图是西安地铁四号线图(部分).乐乐和小敏分别从行政中心(用![]() 表示)、文景路(用
表示)、文景路(用![]() 表示)、凤城九路(用
表示)、凤城九路(用![]() 表示)这三站中,随机选取一站作为调查的站点.
表示)这三站中,随机选取一站作为调查的站点.
(1)在这三站中,求乐乐选取问卷调查的站点是文景路站的概率;
(2)请你用画树状图或列表法,求乐乐和小敏所选取问卷调查的站点相邻的概率.(各站点用相应的字母表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com