
科目: 来源: 题型:
【题目】解题时,最容易想到的方法未必是最简单的,你可以再想一想,尽量优化解法.
例题呈现
关于x的方程a(x+m)2+b=0的解是x1=1,x2=-2(a、m、b均为常数,a≠0),则方程a(x+m+2)2+b=0的解是 .
解法探讨
(1)小明的思路如图所示,请你按照他的思路解决这个问题;
小明的思路
第1步 把1、-2代入到第1个方程中求出m的值;
第2步 把m的值代入到第1个方程中求出![]() 的值;
的值;
第3步 解第2个方程.
(2)小红仔细观察两个方程,她把第2个方程a(x+m+2)2+b=0中的“x+2”看作第1个方程中的“x”,则“x+2”的值为 ,从而更简单地解决了问题.
策略运用
(3)小明和小红认真思考后发现,利用方程结构的特点,无需计算“根的判别式”就能轻松解决以下问题,请用他们说的方法完成解答.
已知方程 (a2-2b2)x2+(2b2-2c2)x+2c2-a2=0有两个相等的实数根,其中a、b、c是△ABC三边的长,判断△ABC的形状.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,O为坐标原点,已知点F(2![]() ,0),直线GF交y轴正半轴于点G,且∠GFO=30°.
,0),直线GF交y轴正半轴于点G,且∠GFO=30°.
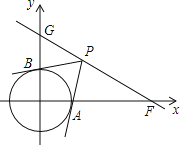
(1)直接写出点G的坐标;
(2)若⊙O的半径为1,点P是直线GF上的动点,直线PA、PB分别约⊙O相切于点A、B.
①求切线长PB的最小值;
②问:在直线GF上是够存在点P,使得∠APB=60°,若存在,请求出P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
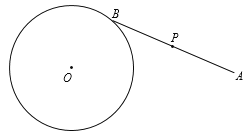
【题目】如图,⊙O的半径为2,O到定点A的距离为5,点B在⊙O上,点P是线段AB的中点.若B在⊙O上运动一周:
(1)证明点P运动的路径是一个圆.
(思路引导:要证点P运动的路径是一个圆,只要证点P到定点M的距离等于定长r,由图中的定点、定长可以发现M、r.)
(2)△ABC始终是一个等边三角形,直接写出PC长的取值范围.
查看答案和解析>>
科目: 来源: 题型:
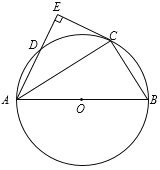
【题目】如图,AB是⊙O的直径,点C、D在圆上,![]() ,过点C作CE⊥AD交AD的延长线于点E.
,过点C作CE⊥AD交AD的延长线于点E.
(1)求证:CE是⊙O的切线;
(2)已知BC=3,AC=4,求CE的长.
查看答案和解析>>
科目: 来源: 题型:
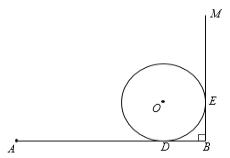
【题目】如图,∠ABM=90°,⊙O分别切AB、BM于点D、E.AC切⊙O于点F,交BM于点C(C与B不重合).
(1)用直尺和圆规作出AC(保留作图痕迹,不写作法);
(2)若⊙O半径为1,AD=4,求AC的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知关于x的一元二次方程 kx2+(2k+1)x+k+2=0.
(1)若该方程有两个不相等的实数根,求k的取值范围;
(2)若该方程的两根x1、x2满足![]() =-3,求k的值.
=-3,求k的值.
查看答案和解析>>
科目: 来源: 题型:
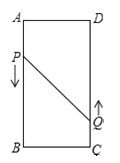
【题目】如图,在矩形ABCD中,AB=16cm,BC=6cm,动点P、Q分别以3cm/s、2cm/s的速度从点A、C同时出发,点Q从点C向点D移动.
(1)若点P从点A移动到点B停止,点Q随点P的停止而停止移动,点P、Q分别从点A、C同时出发,问经过多长时间P、Q两点之间的距离是10cm?
(2)若点P沿着AB→BC→CD移动,点P、Q分别从点A、C同时出发,点Q从点C移动到点D停止时,点P随点Q的停止而停止移动,试探求经过多长时间△PBQ的面积为12cm2?
查看答案和解析>>
科目: 来源: 题型:
【题目】(10分)水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤,为保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四边形ABCD中,BD为一条对角线,AD∥BC,AD=2BC,∠ABD=90°,E为AD的中点,连接BE.
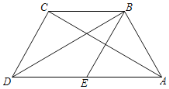
(1)求证:四边形BCDE为菱形;
(2)连接AC,若AC平分∠BAD,AB=2,求菱形BCDE的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com