
科目: 来源: 题型:
【题目】如图,AB是⊙O的直径,点C为半径OA的上的中点,CD⊥AB交⊙O于点D和点E,DF∥AB交⊙O于F,连结AF,AD.
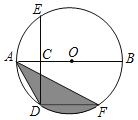
(1)求∠DAF的度数;
(2)若AB=10,求弦AD,AF和![]() 所围成的图形的面积.(结果保留π)
所围成的图形的面积.(结果保留π)
查看答案和解析>>
科目: 来源: 题型:
【题目】一个不透明的口袋里装有分别标有汉字“美”、“丽”、“光”、“明”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.
(1)若从中任取一个球,求摸出球上的汉字刚好是“美”的概率;
(2)甲从中任取一球,不放回,再从中任取一球,请用树状图或列表法,求甲取出的两个球上的汉字恰能组成“美丽”或“光明”的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在下列4×4(边长为1)的网格中,已知△ABC的三个顶点A,B,C在格点上,请分别按不同要求在网格中描出一个格点D,并写出点D的坐标.
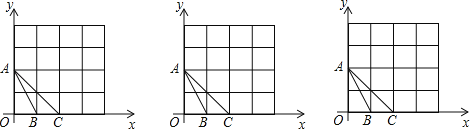
(1)将△ABC绕点C顺时针旋转90°,画出旋转后所得的三角形,点A旋转后落点为D;
(2)经过A,B,C三点有一条抛物线,请找到点D,使点D也落在这条抛物线上;
(3)经过A,B,C三点有一个圆,请找到一个横坐标为2的点D,使点D也落在这个圆上,
①点D的坐标为 ;
②点D的坐标为 ;
③点D的坐标为 .
查看答案和解析>>
科目: 来源: 题型:
【题目】我市倡导垃圾分类投放,将日常垃圾分成四类,分别投放四种不同颜色的垃圾桶中,在“垃圾分类”模拟活动中,某同学把两个不同类的垃圾随意放入两个不同颜色的垃圾筒中,则这个同学正确分类投放垃圾的概率是______.
查看答案和解析>>
科目: 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P和⊙M,给出如下定义:若⊙M上存在两个点A,B,使AB=2PM,则称点P为⊙M的“美好点”.
(1)当⊙M半径为2,点M和点O重合时,
①点P1(-2,0),P2(1,1),P3(2,2)中,⊙O的“美好点”是______;
②点P为直线y=x+b上一动点,点P为⊙O的“美好点”,求b的取值范围;
(2)点M为直线y=x上一动点,以2为半径作⊙M,点P为直线y=4上一动点,点P为⊙M的“美好点”,求点M的横坐标m的取值范围.
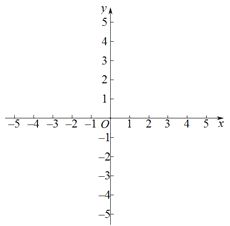
查看答案和解析>>
科目: 来源: 题型:
【题目】已知,在平面直角坐标系xOy中,点A的坐标为(0,2),点P(m,n)是抛物线![]() 上的一个动点.
上的一个动点.
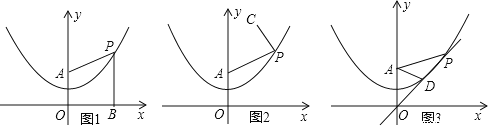
(1)如图1,过动点P作PB⊥x轴,垂足为B,连接PA,请通过测量或计算,比较PA与PB的大小关系:PA_____PB(直接填写“>”“<”或“=”,不需解题过程);
(2)请利用(1)的结论解决下列问题:
①如图2,设C的坐标为(2,5),连接PC,AP+PC是否存在最小值?如果存在,求点P的坐标;如果不存在,简单说明理由;
②如图3,过动点P和原点O作直线交抛物线于另一点D,若AP=2AD,求直线OP的解析式.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点
两点![]() 在
在![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,点
,点![]() 与
与![]() 关于抛物线的对称轴对称.
关于抛物线的对称轴对称.
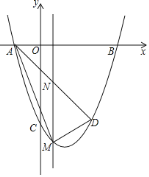
(1)求抛物线的解析式及点![]() 的坐标;
的坐标;
(2)点![]() 是抛物线上的一点,当
是抛物线上的一点,当![]() 的面积是8,求出点
的面积是8,求出点![]() 的坐标;
的坐标;
(3)过直线![]() 下方的抛物线上一点
下方的抛物线上一点![]() 作
作![]() 轴的平行线,与直线
轴的平行线,与直线![]() 交于点
交于点![]() ,已知
,已知![]() 点的横坐标是
点的横坐标是![]() ,试用含
,试用含![]() 的式子表示
的式子表示![]() 的长及△ADM的面积
的长及△ADM的面积![]() ,并求当
,并求当![]() 的长最大时
的长最大时![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
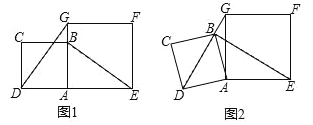
【题目】正方形ABCD和正方形AEFG的边长分别为2和![]() ,点B在边AG上,点D在线段EA的延长线上,连接BE.
,点B在边AG上,点D在线段EA的延长线上,连接BE.
(1)如图1,求证:DG⊥BE;
(2)如图2,将正方形ABCD绕点A按逆时针方向旋转,当点B恰好落在线段DG上时,求线段BE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com