
科目: 来源: 题型:
【题目】我国魏晋时期的数学家刘徽(263年左右)首创“割圆术”,所谓“割圆术”就是利用圆内接正多边形无限逼近圆来确定圆周率,刘徽计算出圆周率![]() .
.

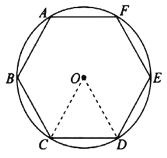
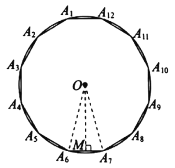
刘徽从正六边形开始分割圆,每次边数成倍增加,依次可得圆内接正十二边形,圆内接正二十四边形,…,割的越细,圆的内接正多边形就越接近圆.设圆的半径为R,圆内接正六边形的周长![]() ,计算
,计算![]() ;圆内接正十二边形的周长
;圆内接正十二边形的周长![]() ,计算
,计算![]() ;请写出圆内接正二十四边形的周长
;请写出圆内接正二十四边形的周长![]() ________,计算
________,计算![]() ________.(参考数据:
________.(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知二次函数![]() 的顶点坐标为
的顶点坐标为![]() ,
,![]() .
.
(1)若该函数图象过点![]() .
.
①求该函数解析式;
②![]() ,函数图象上点
,函数图象上点![]() 到x轴的距离最小值为1,则t的值为______;
到x轴的距离最小值为1,则t的值为______;
(2)若点P在函数![]() 的图象上,且
的图象上,且![]() ,求h的最大值.
,求h的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某商场销售一批名牌衬衫,平均每天能售出20件,每件盈利40元。经调查发现:如果这种衬衫的售价每降低1元时,平均每天能多售出2件.设每件衬衫降价x元.
(1)降价后,每件衬衫的利润为_____元,销量为_____件;(用含x的式子表示)
(2)为了扩大销售,尽快减少库存,商场决定釆取降价措施。但需要平均每天盈利1200元,求每件衬衫应降价多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,已知一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() .
.
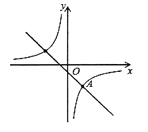
(1)求反比例函数的解析式;
(2)若一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象的另一个交点为
的图象的另一个交点为![]() ,请直接写出关于x的不等式
,请直接写出关于x的不等式![]() 的解集.
的解集.
查看答案和解析>>
科目: 来源: 题型:
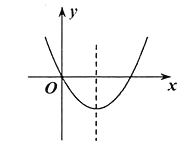
【题目】如图,函数![]() 的图象经过原点,开口向上,对称轴为直线
的图象经过原点,开口向上,对称轴为直线![]() ,对于下列两个结论:①m为任意实数,则有
,对于下列两个结论:①m为任意实数,则有![]() ;②方程
;②方程![]() 有两个不相等的实数根,一个根小于0,另一个根大于2,说法正确的是( )
有两个不相等的实数根,一个根小于0,另一个根大于2,说法正确的是( )
A.①对,②错B.①错,②对C.①②都对D.①②都错
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在某温度不变的条件下,通过一次又一次地对气缸顶部的活塞加压,测出每一次加压后气缸内气体的体积![]() 与气体对气缸壁产生的压强
与气体对气缸壁产生的压强![]() 的关系可以用如图所示的函数图象进行表示,下列说法正确的是( )
的关系可以用如图所示的函数图象进行表示,下列说法正确的是( )
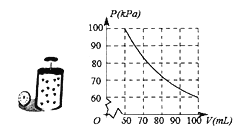
A.气压P与体积V的关系式为![]()
B.当气压![]() 时,体积V的取值范围为
时,体积V的取值范围为![]()
C.当体积V变为原来的一半时,对应的气压P也变为原来的一半
D.当![]() 时,气压P随着体积V的增大而减小
时,气压P随着体积V的增大而减小
查看答案和解析>>
科目: 来源: 题型:
【题目】综合与探究
如图,在平面直角坐标系中,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 的右侧),与
的右侧),与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() .
.
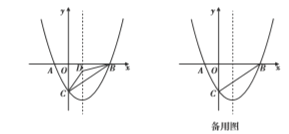
(1)求点![]() 三点的坐标和抛物线的对称轴;
三点的坐标和抛物线的对称轴;
(2)点![]() 为抛物线对称轴上一点,连接
为抛物线对称轴上一点,连接![]() ,
,![]() ,若
,若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)已知点![]() ,若
,若![]() 是抛物线上一个动点(其中
是抛物线上一个动点(其中![]() ),连接
),连接![]() ,
,![]() ,
,![]() ,求
,求![]() 面积的最大值及此时点
面积的最大值及此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】综合与实践
观察猜想

如图1,有公共直角顶点![]() 的两个不全等的等腰直角三角尺叠放在一起,点
的两个不全等的等腰直角三角尺叠放在一起,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上.
上.
(1)在图1中,你发现线段![]() ,
,![]() 的数量关系是___________,直线
的数量关系是___________,直线![]() ,
,![]() 的位置关系是________.
的位置关系是________.
操作发现
(2)将图1中的![]() 绕点
绕点![]() 逆时针旋转一个锐角得到图2,这时(1)中的两个结论是否成立?作出判断并说明理由;
逆时针旋转一个锐角得到图2,这时(1)中的两个结论是否成立?作出判断并说明理由;
拓广探索
(3)如图3,若只把“有公共直角顶点![]() 的两个不全等的等腰直角三角尺”改为“有公共顶角为
的两个不全等的等腰直角三角尺”改为“有公共顶角为![]() (锐角)的两个不全等等腰三角形”,
(锐角)的两个不全等等腰三角形”,![]() 绕点
绕点![]() 逆时针旋转任意一个锐角,这时(1)中的两个结论仍然成立吗?作出判断,不必说明理由.
逆时针旋转任意一个锐角,这时(1)中的两个结论仍然成立吗?作出判断,不必说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某面粉厂生产某品牌的面粉按质量分5个档次,生产第一档(最低档次)面粉,每天能生产55吨,每吨利润1000元.生产面粉的质量每提高一个档次,每吨利润会增加200元,但每天的产量会减少5吨.
(1)若生产第![]() 档次的面粉每天的总利润为
档次的面粉每天的总利润为![]() 元(其中
元(其中![]() 为正整数,且
为正整数,且![]() ),求生产哪个档次的面粉时,每天的利润最大,每天的最大利润是多少元?
),求生产哪个档次的面粉时,每天的利润最大,每天的最大利润是多少元?
(2)若生产第![]() 档次的面粉一天的总利润为60000元,求该面粉的质量档次.
档次的面粉一天的总利润为60000元,求该面粉的质量档次.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com