【题目】某游乐场试营业期间，每天运营成本为1000元.经统计发现，每天售出的门票张数（张）与门票售价（元/张）之间满足一次函数，设游乐场每天的利润为（元）.（利润=票房收入－运营成本）

（1）试求与之间的函数表达式.

（2）游乐场将门票售价定为多少元/张时，每天获利最大？最大利润是多少元？

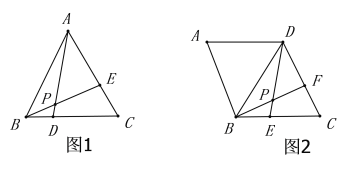
先出示问题（1）:如图1，在等边三角形中，为上一点，为上一点，如果，连接、，、相交于点，求的度数.

通过学习，王老师请同学们说说自己的收获.小明说发现一个结论：在这个等边三角形中，只要满足，则的度数就是一个定值，不会发生改变.紧接着王老师出示了问题（2）:如图2，在菱形中，，为上一点，为上一点，，连接、，、相交于点，如果，，求出菱形的边长.

问题（3）：通过以上的学习请写出你得到的启示（一条即可）.

【题目】在学习了矩形后，数学活动小组开展了探究活动.如图1，在矩形中，，，点在上，先以为折痕将点往右折，如图2所示，再过点作，垂足为，如图3所示.

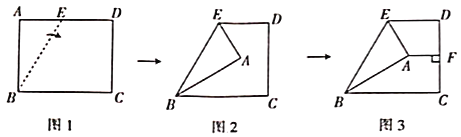
（1）在图3中，若，则的度数为______，的长度为______.

（2）在（1）的条件下，求的长.

（3）在图3中，若，则______.

【题目】如图，直线交轴于点，交轴于点，抛物线经过点，交轴于点，点为抛物线上一动点，过点作轴的垂线，交直线于点，设点的横坐标为.

（1）求抛物线的解析式.

（2）当点在直线下方的抛物线上运动时，求出长度的最大值.

（3）当以，，为顶点的三角形是等腰三角形时，求此时的值.

(1)画出测杆MN在同一时刻的影子NP(用粗线表示)，并简述画法；

(2)若在同一时刻测杆XY的影子的顶端恰好落在点B处，画出测杆XY所在的位置(用实线表示)，并简述画法．

（1）请你确定灯泡所在的位置，并画出小亮在灯光下形成的影子．

（2）如果小明的身高AB=1.6m，他的影子长AC=1.4m，且他到路灯的距离AD=2.1m，求灯泡的高.

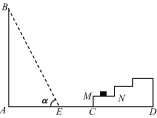
(1)求楼房的高度约为多少米?(结果精确到0.1米)

(2)过了一会儿,当α=45°时,小猫还能不能晒到太阳?请说明理由.(参考数据:≈1.732)

【题目】直线与轴交于点，与轴交于点，抛物线经过两点.

（1）求这个二次函数的表达式；

（2）若是直线上方抛物线上一点；

①当的面积最大时，求点的坐标；

②在①的条件下，点关于抛物线对称轴的对称点为，在直线上是否存在点，使得直线与直线的夹角是的两倍，若存在，直接写出点的坐标，若不存在，请说明理由.

【题目】我市某公司用800万元购得某种产品的生产技术后，进一步投入资金1550万元购买生产设备，进行该产品的生产加工，已知生产这种产品每件还需成本费40元.经过市场调研发现：该产品的销售单价需要定在200元到300元之间较为合理.销售单价（元）与年销售量（万件）之间的变化可近似的看作是如下表所反应的一次函数：

（1）请求出与之间的函数关系式，并直接写出自变量的取值范围；

（2）请说明投资的第一年，该公司是盈利还是亏损？若盈利，最大利润是多少？若亏损，最少亏损是多少？

（1）学生小红计划选修两门课程，请写出所有可能的选法；

（2）若学生小明和小刚各计划送修一门课程，则他们两人恰好选修同一门课程的概率为多少？