
科目: 来源: 题型:
【题目】小飞文具店今年7月份购进一批笔记本,共2290本,每本进价为10元,该文具店决定从8月份开始进行销售,若每本售价为11元,则可全部售完;且每本售价每增长1元,销量就减少30本.
(1)若该种笔记本在8月份的销售量不低于2200本,则8月份售价应不高于多少元?
(2)由于生产商提高造纸工艺,该笔记本的进价提高了10%,文具店为了增加笔记本的销量进行了销售调整,售价比8月份在(1)的条件下的最高售价减少了![]() m%,结果9月份的销量比8月份在(1)的条件下的最低销量增加了m%,9月份的销售利润达到6600元,求m的值.
m%,结果9月份的销量比8月份在(1)的条件下的最低销量增加了m%,9月份的销售利润达到6600元,求m的值.
查看答案和解析>>
科目: 来源: 题型:
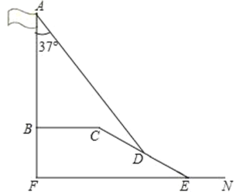
【题目】在学习解直角三角形以后,重庆八中数学兴趣小组测量了旗杆的高度,如图,某一时刻,旗杆AB的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长BC为6米,落在斜坡上的影长CD为4米,AB⊥BC,同一时刻,光线与旗杆的夹角为37°,斜坡CE的坡角为30°,旗杆的高度约为多少米?(结果精确到0.1,参考数据:sin37°=0.60,cos37°≈0.80,tan37°≈0.75,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目: 来源: 题型:
【题目】2018年9月28日,重庆八中80周年校庆在渝北校区隆重举行,学校总务处购买了红,黄,蓝三种花卉装扮出甲,乙,丙,丁四种造型,其中一个甲造型需要15盆红花,10盆黄花,10盆蓝花;一个乙造型需要5盆红花,7盆黄花,6盆蓝花;一个丙造型需要7盆红花,8盆黄花,9盆蓝花;一个丁造型需要6盆红花,4盆黄花,4盆蓝花,若一个甲造型售价1800元,利润率为20%,一个乙和一个丙造型一共成本和为1830元,且一盆红花的利润率为25%,问一个丁造型的利润率为_____.
查看答案和解析>>
科目: 来源: 题型:
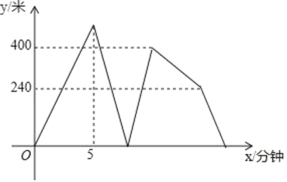
【题目】春天的某个周末,阳光明媚,适合户外运动.下午,住在同一小区的小懿、小静两人不约而同的都准备从小区出发,沿相同的路线步行去同一个公园赏花!小懿出发5分钟后小静才出发,同时小懿发现当天的光线很适合摄影,所以决定按原速回家拿相机,小懿拿了相机后,担心错过最佳拍照时间,所以速度提高了20%,结果还是比小静晚2分钟到公园.小懿取相机的时间忽略不计,在整个过程中,小静保持匀速运动,小懿提速前后也分别保持匀速运动.如图所示是小懿、小静之间的距离y(米)与小懿离开小区的时间x(分钟)之间的函数图象,则小区到公园的距离为_____米.
查看答案和解析>>
科目: 来源: 题型:
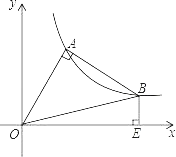
【题目】△OAB在第一象限中,OA=AB,OA⊥AB,O是坐标原点,且函数y=![]() 正好过A,B两点,BE⊥x轴于E点,则OE2﹣BE2的值为( )
正好过A,B两点,BE⊥x轴于E点,则OE2﹣BE2的值为( )
A. 3B. 2C. 3D. 4
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,函数图象![]() 上点
上点![]() 的横坐标
的横坐标![]() 与其纵坐标
与其纵坐标![]() 的和
的和![]() 称为点
称为点![]() 的“坐标和”,而图象
的“坐标和”,而图象![]() 上所有点的“坐标和”中的最小值称为图象
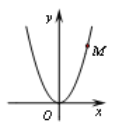
上所有点的“坐标和”中的最小值称为图象![]() 的“智慧数”.如图:抛物线
的“智慧数”.如图:抛物线![]() 上有一点
上有一点![]() ,则点
,则点![]() 的“坐标和”为6,当
的“坐标和”为6,当![]() 时,该抛物线的“智慧数”为0.
时,该抛物线的“智慧数”为0.
(1)点![]() 在函数
在函数![]() 的图象上,点
的图象上,点![]() 的“坐标和”是 ;
的“坐标和”是 ;
(2)求直线![]() 的“智慧数”;
的“智慧数”;
(3)若抛物线![]() 的顶点横、纵坐标的和是2,求该抛物线的“智慧数”;
的顶点横、纵坐标的和是2,求该抛物线的“智慧数”;
(4)设抛物线![]() 顶点的横坐标为
顶点的横坐标为![]() ,且该抛物线的顶点在一次函数
,且该抛物线的顶点在一次函数![]() 的图象上;当
的图象上;当![]() 时,抛物线
时,抛物线![]() 的“智慧数”是2,求该抛物线的解析式.
的“智慧数”是2,求该抛物线的解析式.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下面材料,完成(1),(2)两题
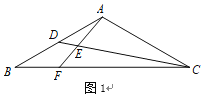
数学课上,老师出示了这样一道题:如图1,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 上一点,且满足
上一点,且满足![]() ,
,![]() 为
为![]() 上一点,
上一点,![]() ,延长
,延长![]() 交
交![]() 于
于![]() ,求
,求![]() 的值.同学们经过思考后,交流了自己的想法:
的值.同学们经过思考后,交流了自己的想法:
小明:“通过观察和度量,发现![]() 与
与![]() 相等.”
相等.”
小伟:“通过构造全等三角形,经过进一步推理,就可以求出![]() 的值.”
的值.”
……
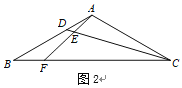
老师:“把原题条件中的‘![]() ’,改为‘
’,改为‘![]() ’其他条件不变(如图2),也可以求出
’其他条件不变(如图2),也可以求出![]() 的值.
的值.
(1)在图1中,①求证:![]() ;②求出
;②求出![]() 的值;
的值;
(2)如图2,若![]() ,直接写出
,直接写出![]() 的值(用含
的值(用含![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,点
,点![]() 是射线
是射线![]() 上一动点(点
上一动点(点![]() 不与点
不与点![]() ,
,![]() 重合),过点
重合),过点![]() 作
作![]() 垂直于
垂直于![]() 轴,交直线
轴,交直线![]() 于点
于点![]() ,以直线
,以直线![]() 为对称轴,将
为对称轴,将![]() 翻折,点
翻折,点![]() 的对称点
的对称点![]() 落在
落在![]() 轴上,以
轴上,以![]() ,
,![]() 为邻边作平行四边形
为邻边作平行四边形![]() .设点
.设点![]() ,
,![]() 与
与![]() 重叠部分的面积为
重叠部分的面积为![]() .
.

(1)![]() 的长是__________,
的长是__________,![]() 的长是___________(用含
的长是___________(用含![]() 的式子表示);
的式子表示);
(2)求![]() 关于
关于![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com