
科目: 来源: 题型:
【题目】设某工厂生产的一种产品的一项质量指标值![]() 服从正态分布
服从正态分布![]() ,若一件产品的质量指标值
,若一件产品的质量指标值![]() 介于90到120之间时,称该产品为优质品.
介于90到120之间时,称该产品为优质品.
(1)计算该工厂生产的这种产品的优质品率![]() .
.
(2)某用户从该工厂购买了100件这种产品,记![]() 表示这100件产品中优质品的件数,求随机变量
表示这100件产品中优质品的件数,求随机变量![]() 的数学期望
的数学期望![]() .
.
(3)必须从这工厂中购买多少件产品,才能使其中至少有1件产品是优质品的概率大于0.9?
①参考数据:若随机变量![]() ),则
),则![]() ,
,![]() ,
,![]() .
.
②计算时,所有的小数都精确到小数点后4位,例如:![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司的营销部门对某件商品在网上销售情况进行调查,发现当这件商品每回馈消费者一定的点数,该商品每天的销量就会发生一定的变化,经过统计得到以下表:
![]()
(1)经分析发现,可用线性回归模型拟合该商品销量![]() (百件)与返还点数
(百件)与返还点数![]() 之间的相关关系.请用最小二乘法求
之间的相关关系.请用最小二乘法求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测若返回6个点时该商品每天销量;
,并预测若返回6个点时该商品每天销量;
(2)该公司为了在购物节期间对所有商品价格进行新一轮调整,随机抽查了上一年购物节期间60名网友的网购金额情况,得到如下数据统计表:
网购金额 (单位:千元) |
|
|
|
|
|
| 合计 |
频数 | 3 | 9 | 9 | 15 | 18 | 6 | 60 |
若网购金额超过2千元的顾客定义为“网购达人”,网购金额不超过2千元的顾客定义为“非网购达人”.该营销部门为了进步了解这60名网友的购物体验,从“非网购达人”、“网购达人”中用分层抽样的方法确定10人,若需从这10人中随机选取3人进行问卷调查.设![]() 为选取的3人中“网购达人”的人数,求
为选取的3人中“网购达人”的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考公式及数据:①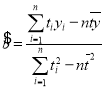 ,
,![]() ;②
;②![]() .
.
查看答案和解析>>
科目: 来源: 题型:
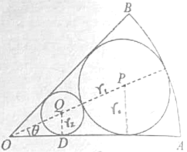
【题目】如图,在半径为常量![]() ,圆心角为变量
,圆心角为变量![]() 的扇形
的扇形![]() 内作一内切圆
内作一内切圆![]() ,再在扇形内作一个与扇形两半径相切并与圆
,再在扇形内作一个与扇形两半径相切并与圆![]() 外切的小圆
外切的小圆![]() ,设圆
,设圆![]() 的半径为
的半径为![]() ,则
,则![]() 的半径为
的半径为![]() .
.
(1)求![]() 的取值范围;
的取值范围;
(2)求圆![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】随机调查某社区80个人,以研究这一社区居民在晚上8点至十点时间段的休闲方式与性别的关系,得到下面的数据表:

(1)将此样本的频率估计为总体的概率,随机调查3名在该社区的男性,求这3人中至少有1人是以看书为休闲方式的概率;
(2)根据以上数据,能否有99%的把握认为“在晚上8点至十点时间段的休闲方式与性别有关系?”
参考公式: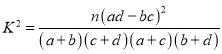 ,其中
,其中![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目: 来源: 题型:
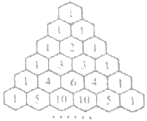
【题目】如图所示,在“杨辉三角”中,去除所有为1的项,依次构成数列2,3,3,4,6,4,5,10,10,5,…,则此数列前21项的和为_______________.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知圆C的圆心C在直线![]() 上,且与x轴正半轴相切,点C与坐标原点O的距离为
上,且与x轴正半轴相切,点C与坐标原点O的距离为![]() .
.
(1)求圆C的标准方程;
(2)直线l过点 ![]() 且与圆C相交于A,B两点,求弦长
且与圆C相交于A,B两点,求弦长![]() 的最小值及此时直线l的方程.
的最小值及此时直线l的方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是矩形,侧棱PD⊥底面ABCD,PD=DC,点E是PC的中点,作EF⊥PB交PB于点F.
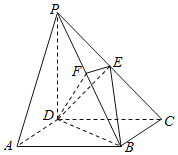
(1)求证:PA∥平面BDE;
(2)求证:PB⊥平面DEF.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() ,其导函数设为
,其导函数设为![]() .
.
(Ⅰ)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)若函数![]() 有两个极值点
有两个极值点![]() ,
,![]() ,试用
,试用![]() 表示
表示![]() ;
;
(Ⅲ)在(Ⅱ)的条件下,若![]() 的极值点恰为
的极值点恰为![]() 的零点,试求
的零点,试求![]() ,
,![]() 这两个函数的所有极值之和的取值范围.
这两个函数的所有极值之和的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com