
科目: 来源: 题型:
【题目】根据以往统计资料,某地车主购买甲种保险的概率为0.5,购买乙种保险但不购买甲种保险的概率为0.3.设各车主购买保险相互独立.
(1)求该地1位车主至少购买甲、乙两种保险中的1种的概率;
(2)X表示该地的100位车主中,甲、乙两种保险都不购买的车主数,求X的均值和方差.
查看答案和解析>>
科目: 来源: 题型:
【题目】铁人中学高二学年某学生对其亲属30人![]() 饮食习惯进行了一次调查,并用如图所示的茎叶图表示30人的饮食指数.(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主.)
饮食习惯进行了一次调查,并用如图所示的茎叶图表示30人的饮食指数.(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主.)
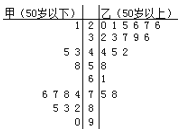
(Ⅰ)根据茎叶图,帮助这位学生说明其亲属30人的饮食习惯;
(Ⅱ)根据以上数据完成下列![]() 的列联表:
的列联表:
主食蔬菜 | 主食肉类 | 合计 | |
50岁以下人数 | |||
50岁以上人数 | |||
合计人数 |
(Ⅲ)能否在犯错误的概率不超过0.01的前提下认为其亲属的饮食习惯与年龄有关系?
附:![]() .
.
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】从甲地到乙地要经过3个十字路口,设各路口信号灯工作相互独立,且在各路口遇到红灯的概率分别为![]() .
.
(Ⅰ)设![]() 表示一辆车从甲地到乙地遇到红灯的个数,求随机变量
表示一辆车从甲地到乙地遇到红灯的个数,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅱ)若有2辆车独立地从甲地到乙地,求这2辆车共遇到1个红灯的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线C的方程为
中,曲线C的方程为![]() ,以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,直线l的极坐标方程为
,以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,直线l的极坐标方程为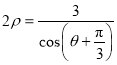 .
.
(1)求直线l的直角坐标方程和曲线C的参数方程;
(2)已知P、Q两点分别是曲线C和直线l上的动点,且直线![]() 的倾斜角为
的倾斜角为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知点![]() 为椭圆C:
为椭圆C:![]() (
(![]() ,
,![]() )上一点,
)上一点,![]() 和
和![]() 分别为椭圆C的左右焦点,点D为椭圆C的上顶点,且
分别为椭圆C的左右焦点,点D为椭圆C的上顶点,且![]() .
.
(1)椭圆C的方程;
(2)若点A、B、P为椭圆C上三个不同的动点,且满足![]() ,直线
,直线![]() 与直线
与直线![]() 交于点Q,试判断动点Q的轨迹与直线
交于点Q,试判断动点Q的轨迹与直线![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了响应绿色出行,某市推出了新能源分时租赁汽车,并对该市市民使用新能源租赁汽车的态度进行调查,得到有关数据如下表1:
表1
愿意使用新能源租赁汽车 | 不愿意使用新能源租赁汽车 | 总计 | |
男性 | 100 | 300 | |
女性 | 400 | ||
总计 | 400 |
其中一款新能源分时租赁汽车的每次租车费用由行驶里程和用车时间两部分构成:行驶里程按1元/公里计费;用车时间不超过30分钟时,按0.15元/分钟计费;超过30分钟时,超出部分按0.20元/分钟计费.已知张先生从家到上班地点15公里,每天上班租用该款汽车一次,每次的用车时间均在20~60分钟之间,由于堵车红绿灯等因素,每次的用车时间![]() (分钟)是一个随机变量.张先生记录了100次的上班用车时间,并统计出在不同时间段内的频数如下表2:
(分钟)是一个随机变量.张先生记录了100次的上班用车时间,并统计出在不同时间段内的频数如下表2:
表2
时间 | (20,30] | (30,40] | (40,50] | (50,60] |
频数 | 20 | 40 | 30 | 10 |
(1)请补填表1中的空缺数据,并判断是否有99.5%的把握认为该市市民对新能源租赁汽车的使用态度与性别有关;
(2)根据表2中的数据,将各时间段发生的频率视为概率,以各时间段的区间中点值代表该时间段的取值,试估计张先生租用一次该款汽车上班的平均用车时间;
附: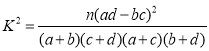
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com