|
试题详情
试题详情
试题详情
二、填空题:本大题共7小题,每小题5分,满分30分.本大题分为必做题和选做题两部分. (一)必做题:第9、10、11、12题为必做题,每道试题考生都必须做答 试题详情
试题详情
试题详情
 11.为了调查某厂工人生产某种产品的能力,随机 11.为了调查某厂工人生产某种产品的能力,随机
抽查了20位工人某天生产该产品的数量.产品数 试题详情
量的分组区间为 , ,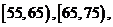 试题详情
 , , 由此得到频率分布直方图如 由此得到频率分布直方图如
图,则由此估计该厂工人一天生产该产品数量在 试题详情
 的人数约占该厂工人总数的百分率是 . 的人数约占该厂工人总数的百分率是 .
试题详情
试题详情
(二)选做题:第13、14、15题为选做题,考生只能选做两题,三题全答的,只计算前两题的得分. 试题详情
试题详情
试题详情
试题详情
试题详情
已知 ,且 ,且 , , 试题详情
则 =___________. =___________. 试题详情
三、解答题:本大题6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.
试题详情
试题详情
(Ⅰ) 求 ; ; 试题详情
(Ⅱ) 求 的长. 的长. 试题详情
试题详情
某商场为刺激消费,拟按以下方案进行促销:顾客每消费500元便得到抽奖券一张,每张抽奖券的中奖概率为 ,若中奖,商场返回顾客现金100元.某顾客现购买价格为2300的台式电脑一台,得到奖券4张. ,若中奖,商场返回顾客现金100元.某顾客现购买价格为2300的台式电脑一台,得到奖券4张. 试题详情
(Ⅰ)设该顾客抽奖后中奖的抽奖券张数为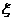 ,求 ,求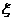 的分布列; 的分布列; 试题详情
(Ⅱ)设该顾客购买台式电脑的实际支出为 (元),用 (元),用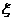 表示 表示 ,并求 ,并求 的数学期望. 的数学期望. 试题详情
试题详情
试题详情
试题详情
(Ⅰ)求 两点间的距离; 两点间的距离; 试题详情
(Ⅱ)证明: 平面 平面 ; ; 试题详情
试题详情
试题详情
试题详情
(Ⅰ)求曲线 的方程; 的方程; 试题详情
(Ⅱ)线段 是曲线 是曲线 的长为 的长为 的动弦, 的动弦, 为坐标原点,求 为坐标原点,求 面积 面积 的取值范围. 的取值范围. 试题详情
试题详情
试题详情
 (Ⅰ)求证:数列 (Ⅰ)求证:数列 为等差数列; 为等差数列;
试题详情
(Ⅱ)求数列 的通项公式; 的通项公式; 试题详情
(Ⅲ)求下表中前 行所有数的和 行所有数的和 . .
试题详情
试题详情
已知函数 (常数 (常数 . . 试题详情
试题详情
(Ⅱ)讨论函数 在区间 在区间 上零点的个数( 上零点的个数( 为自然对数的底数). 为自然对数的底数). 2009年深圳市高三年级第二次调研考试 数学(理科)答案及评分标准 说明: 1 2 3 4 5 6 7 8 C A A B D C A D 试题详情
二、填空题:本大题每小题5分(第12题前空2分,后空3分),满分30分.
试题详情
试题详情
三、解答题:本大题6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.
试题详情
试题详情
(Ⅰ) 求 ; ; 试题详情
(Ⅱ) 求 的长. 的长. 试题详情
解:(Ⅰ)在 中, 中, 试题详情
 . .
试题详情
 . …………………………2分 . …………………………2分
试题详情
从而 …………………………6分
…………………………6分 试题详情
∴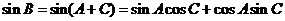  ……9分 ……9分 (Ⅱ)由正弦定理可得 试题详情
 , ,
试题详情
 …………………………12分
…………………………12分
试题详情
试题详情
某商场为刺激消费,拟按以下方案进行促销:顾客每消费500元便得到抽奖券一张,每张抽奖券的中奖概率为 ,若中奖,商场返回顾客现金100元.某顾客现购买价格为2300的台式电脑一台,得到奖券4张. ,若中奖,商场返回顾客现金100元.某顾客现购买价格为2300的台式电脑一台,得到奖券4张. 试题详情
(Ⅰ)设该顾客抽奖后中奖的抽奖券张数为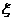 ,求 ,求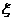 的分布列; 的分布列; 试题详情
试题详情
解:(Ⅰ)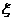 的所有可能值为0,1,2,3,4.…………………………1分 的所有可能值为0,1,2,3,4.…………………………1分 试题详情
 , ,
试题详情
 , ,
试题详情
试题详情
 , ,
试题详情
 .
……………………4分 .
……………………4分
其分布列为: 试题详情
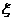
0 1 2 3 4 试题详情
试题详情
试题详情
试题详情
试题详情
试题详情

…………………………6分 试题详情
(Ⅱ) , , 试题详情
 .
…………………………8分 .
…………………………8分 由题意可知 试题详情
 ,
…………………………10分 ,
…………………………10分
试题详情
 元. …………………………12分 元. …………………………12分
试题详情
试题详情
(Ⅰ)求 两点间的距离; 两点间的距离; 试题详情
试题详情
 (Ⅲ)求直线 (Ⅲ)求直线 与平面 与平面 所成角的正弦值. 所成角的正弦值.
(图一) (图二) 试题详情
试题详情
由 ,得: ,得: 试题详情
试题详情
 就是二面角 就是二面角 的平面角, 的平面角,
试题详情
 …………………………2分
…………………………2分
试题详情
在 中, 中,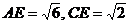 试题详情
试题详情
试题详情
 …………………………4 分
…………………………4 分
试题详情
(Ⅱ)由 , ,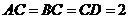 试题详情
试题详情
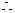  …………………………6分 …………………………6分
试题详情
 , ,
试题详情
又 试题详情
 平面 平面 .
…………………………8分 .
…………………………8分
试题详情
(Ⅲ)方法一:由(Ⅰ)知 平面 平面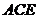 试题详情
 平面 平面
试题详情
∴平面 平面 平面 …………………………10分
…………………………10分 试题详情
平面 平面 平面 , , 试题详情
试题详情
试题详情
 .
…………………………14分 .
…………………………14分
试题详情
试题详情
∵ …………………10分
…………………10分 试题详情
试题详情
 ……………………12分
……………………12分
试题详情
试题详情
 .
………………………14分 .
………………………14分
试题详情
试题详情
  . ………10分 . ………10分
试题详情
设平面 的法向量为n 的法向量为n ,则 ,则 试题详情
试题详情
取 ,则n ,则n ,
----------12分 ,
----------12分 试题详情
试题详情
 . ……………14分 . ……………14分
试题详情
试题详情
试题详情
(Ⅰ)求曲线 的方程; 的方程; 试题详情
试题详情
解:(Ⅰ)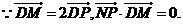 试题详情
试题详情
又 ………………………………3分 ………………………………3分 试题详情
试题详情
∴轨迹E的方程为 ………………………………………………………5分 ………………………………………………………5分 试题详情
试题详情
由 ,消去 ,消去 ,并整理,得 ,并整理,得 试题详情
试题详情
设 , , ,则 ,则 试题详情
 , , …………………………………………8分 …………………………………………8分
试题详情
试题详情
试题详情
 , ,
试题详情
试题详情
 ,
………………………………………………………11分 ,
………………………………………………………11分
试题详情
试题详情
 . ………………………………………………12分 . ………………………………………………12分
试题详情
试题详情
试题详情
试题详情
 , ,
试题详情
 . …………………………………………14分 . …………………………………………14分
试题详情
试题详情
由 ,消去 ,消去 ,并整理,得 ,并整理,得 试题详情
试题详情
设 , , ,则 ,则 试题详情
 , , …………………………………………8分 …………………………………………8分
试题详情
试题详情
试题详情
 , ,
试题详情
试题详情
 ………………………………………………………11分
………………………………………………………11分
试题详情
试题详情
试题详情
试题详情
设 ,则 ,则 试题详情
试题详情
 , ,
试题详情
 .
……………………………………………………14分 .
……………………………………………………14分
(注:上述两种解法用均值不等式求解可参照此标准给分) 试题详情
试题详情
试题详情
 (Ⅰ)求证:数列 (Ⅰ)求证:数列 为等差数列; 为等差数列;
试题详情
(Ⅱ)求数列 的通项公式; 的通项公式; 试题详情
(Ⅲ)求下表中前 行所有数的和 行所有数的和 . . 试题详情
试题详情
试题详情
∴ 数列 为等差数列.
……………………………………3分 为等差数列.
……………………………………3分 试题详情
(Ⅱ)由(Ⅰ)得 ……………………………………4分
……………………………………4分 试题详情
试题详情
∴ …………………………………… 8分
…………………………………… 8分 试题详情
试题详情
∴ 第 行各数之和 行各数之和 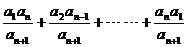 试题详情
 ( ( )……………………12分 )……………………12分
试题详情
∴ 表中前 行所有数的和 行所有数的和 试题详情
试题详情
试题详情
  .
……………………14分 .
……………………14分
试题详情
试题详情
已知函数 (常数 (常数 . . 试题详情
试题详情
试题详情
解:(Ⅰ)当  时, 时, 试题详情
 .
…………………………1分 .
…………………………1分
试题详情
 . .
试题详情
又 , ,
试题详情
试题详情
即 .
……………………………3分 .
……………………………3分 试题详情
(Ⅱ)(1)下面先证明: . . 试题详情
设  ,则 ,则 试题详情
 , ,
试题详情
且仅当 , , 试题详情
所以, 在 在 上是增函数,故 上是增函数,故 试题详情
 . .
试题详情
所以, ,即 ,即 . ……………………………5分 . ……………………………5分 试题详情
(2)因为 ,所以 ,所以 试题详情
试题详情
 . .
试题详情
试题详情
又 , , 试题详情
试题详情
所以, …………………………9分 …………………………9分 试题详情
(3)下面讨论函数 的零点情况. 的零点情况. 试题详情
试题详情
试题详情
试题详情
∴ 在 在 上有一个零点; 上有一个零点; 试题详情
试题详情
由于 , , , , 试题详情
  , ,
试题详情
所以,函数 在 在 上有两个零点. ……………………………………13分 上有两个零点. ……………………………………13分 试题详情
试题详情
解法二:(Ⅱ)依题意,可知函数 的定义域为 的定义域为 , , 试题详情
试题详情
 . ………………………………………5分 . ………………………………………5分 试题详情
试题详情
试题详情
 ………………………………………6分
………………………………………6分
试题详情
试题详情
试题详情
∴当 时, 时,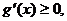 试题详情
且仅当 时, 时,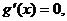 试题详情
 在 在 上是增函数. 上是增函数.
试题详情
∴当 时, 时, , , 试题详情
∴当 时, 时,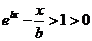 试题详情
试题详情
取 得 得 由此得 由此得 试题详情
  . …………………………10分 . …………………………10分
试题详情
试题详情
试题详情
试题详情
∴函数 有一个零点;
………………………………12分 有一个零点;
………………………………12分 试题详情
试题详情
试题详情
∴函数 有两个零点.
………………………… 有两个零点.
………………………… ……………13分 ……………13分 试题详情
综上所述,当 时,函数 时,函数 无零点,当 无零点,当 时,函数 时,函数 有一个零点,当 有一个零点,当 时,函数 时,函数 有两个零点.
………………14分 有两个零点.
………………14分 命题人:李志敏、胡远东、张松柏 审题人:石永生 试题详情
| 
 , 其中
, 其中 是锥体的底面积,
是锥体的底面积,  是锥体的高.
是锥体的高. 是虚数单位,则
是虚数单位,则
 B.
B. C.
C. D.
D.
 且
且 ,
, ,那么“
,那么“ ”是“
”是“ ”的
”的  充分而不必要条件
充分而不必要条件
 必要而不充分条件
必要而不充分条件 充分必要条件
充分必要条件  既不充分也不必要条件
既不充分也不必要条件 ,
, ,
, ,则
,则 的大小关系是
的大小关系是 







 按
按 元/
元/ 收费,超过
收费,超过 的
的 部分按
部分按 元/
元/ 收费.相应收费系统的流程图如右图所
收费.相应收费系统的流程图如右图所







 ,其底面用斜二测画法所画出的水平放置的直观图是一个边长为1的正方形, 则此四棱锥的体积为
,其底面用斜二测画法所画出的水平放置的直观图是一个边长为1的正方形, 则此四棱锥的体积为








 在直线
在直线 上移动,当
上移动,当 取最小值时,过点
取最小值时,过点 引圆
引圆 的切线,则此切线长等于
的切线,则此切线长等于








 的图象关于直线
的图象关于直线 对称,
对称, 则
则 的值为
的值为  -1
-1  0
0
 1
1  2
2