(第8题) 题号 1 2 3 4 5 6 7 8 答案 B C D D C B A C 第二卷 非选择题(共110分)
试题详情
二、填空题:本大题共7小题,每小题5分,满分30分.其中13~15题是选做题,考生只能选做二题,三题全答的,只计算前两题得分. 9.已知某校的初中学生人数、高中学生人数、教师人数之比为20:15:2,若教师人数为120人,现在用分层抽样的方法从所有师生中抽取一个容量为N的样本进行调查,若应从高中学生中抽取60人,则N=  。 。 试题详情
试题详情
11.已知ΔAOB中,点P在直线AB上,且满足: , , 试题详情
则 = =  。 。 试题详情
 12. 12.
试题详情
试题详情
13.(坐标系与参数方程选做题)极坐标系下,直线 与圆 与圆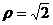 试题详情
的公共点个数是___ ____. ____. 试题详情
14.(不等式选讲选做题)已知关于x的不等式 在x∈(a,+∞)上恒成立, 在x∈(a,+∞)上恒成立, 试题详情
 则实数a的最小值为 则实数a的最小值为  . .
试题详情
15.(几何证明选讲选做题)如图所示, AB是半径等于3 试题详情
的 的直径,CD是 的直径,CD是 的弦,BA,DC的延长线交于点P, 的弦,BA,DC的延长线交于点P, 试题详情
若PA=4,PC=5,则 __ __ ______ ______ 试题详情
三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分)已知函数 , , , , (1)求实数a的值; 试题详情
(2)求函数 在 在 的值域。 的值域。 试题详情
解法1: , , 试题详情
即: ,………………………..2分 ,………………………..2分 试题详情
解得: ; ; 试题详情
 。……………………………..3分 。……………………………..3分
试题详情
(2)由(1)得: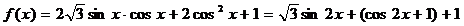
……………….…..5分 试题详情
 ………….…………7分 ………….…………7分 试题详情
 ,…………………………………………..8分 ,…………………………………………..8分
试题详情
令 ,则 ,则 ,…10分 ,…10分 试题详情
 , ,
试题详情
即 …………………………….12分 …………………………….12分 试题详情
解法2: , , 试题详情
即: ,………………………..2分 ,………………………..2分 试题详情
解得: ; ; 试题详情
 。……………………………..3分 。……………………………..3分
试题详情
(2)由(1)得: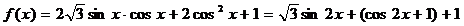
……………….…..5分 试题详情
 ………….…………7分 ………….…………7分 试题详情
 ,…………………………………………..8分 ,…………………………………………..8分
试题详情
令 ,则 ,则 ,…10分 ,…10分 试题详情
 , ,
试题详情
即 …………………………….12分 …………………………….12分 试题详情
解法3:(1)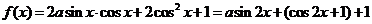 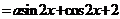 ……………………….2分 试题详情
 ,即: ,即: ,………..4分 ,………..4分
试题详情
解得: ; ;
 。……………………………..5分 。……………………………..5分 试题详情
(2)由(1)得: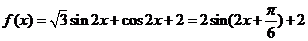 试题详情
或 …………………………………7分 …………………………………7分
以下同解法1或解法2。 试题详情
17.(本小题满分12分)某俱乐部举行迎圣诞活动,每位会员交50元活动费,可享受20元的消费,并参加一次游戏:掷两颗正方体骰子,点数之和为12点获一等奖,奖价值为a元的奖品;点数之和为11或10点获二等奖,奖价值为100元的奖品;点数之和为9或8点获三等奖,奖价值为30元的奖品;点数之和小于8点的不得奖。求: (1)同行的三位会员一人获一等奖、两人获二等奖的概率; (2)如该俱乐部在游戏环节不亏也不赢利,求a的值。 试题详情
解:(1)设掷两颗正方体骰子所得的点数记为(x,y),其中 , , 试题详情
则获一等奖只有(6,6)一种可能,其概率为: ; …………2分 ; …………2分 试题详情
获二等奖共有(6,5)、(5,6)、(4,6)、(6,4)、(5,5)共5种可能,其概率为: ; ;
…………5分 设事件A表示“同行的三位会员一人获一等奖、两人获二等奖”,则有: 试题详情
P(A)= ;
…………6分 ;
…………6分 ξ 30-a -70 0 30 p 试题详情
试题详情
试题详情
试题详情
试题详情
(2)设俱乐部在游戏环节收益为ξ元,则ξ的可能取值为 , , ,0, ,0, ,…7分 ,…7分 其分布列为: 试题详情
则:Eξ= ; …………11分 ; …………11分 由Eξ=0得:a=310,即一等奖可设价值为310 元的奖品。 …………12分 试题详情
试题详情
试题详情
(2)求二面角 的余弦值。 的余弦值。 试题详情
解法1:(1)联结 , , 试题详情
试题详情
∴ ,………………………………….2分 ,………………………………….2分 试题详情
∴ 为 为 中点,……………………………………..3分 中点,……………………………………..3分 试题详情
∵ 为 为 中点, 中点, 试题详情
∴ ,………………………………………….4分 ,………………………………………….4分 试题详情
∴ 平面 平面 …………………………………….5分 …………………………………….5分 试题详情
(2)联结 , , 试题详情
∵ , , 试题详情
∴在等边三角形 中,中线 中,中线 ,…………6分 ,…………6分 试题详情
试题详情
∴ ,………………………………….7分 ,………………………………….7分 试题详情
∴平面 平面 平面 。…………………….8分 。…………………….8分 试题详情
试题详情
试题详情
试题详情
∴ 是二面角 是二面角 的平面角……………….10分 的平面角……………….10分 试题详情
试题详情
试题详情
∴ . . 试题详情
∴二面角 的余弦值为 的余弦值为 。……………….14分 。……………….14分 解法2: 试题详情
试题详情
∵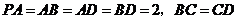 试题详情
∴ ,…………………………………2分 ,…………………………………2分 试题详情
试题详情
试题详情
(1) …………………5分 …………………5分 试题详情
∴ , , 试题详情
试题详情
(2)设平面 的法向量分别为 的法向量分别为 ,.………9分 ,.………9分 试题详情
则 的夹角的补角就是二面角 的夹角的补角就是二面角 的平面角;……………….………10分 的平面角;……………….………10分 试题详情
试题详情
试题详情
 , ,
试题详情
∴二面角 的余弦值为 的余弦值为 。….……………………………………………14分 。….……………………………………………14分 试题详情
试题详情
试题详情
(2)设 ,证明: ,证明: 为常数. 为常数. 试题详情
解:(1)由已知, ,…………………2分 ,…………………2分 试题详情
解得: ,
…………………4分 ,
…………………4分 试题详情
试题详情
(2)解法1:设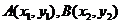 试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
同理由 得: 得: , …………………………………………………12分 , …………………………………………………12分 试题详情
试题详情
故 为常数. ……………………………………………………………………14分 为常数. ……………………………………………………………………14分 试题详情
试题详情
试题详情
试题详情
试题详情
则: ,其中e的离心率;
…………………………12分 ,其中e的离心率;
…………………………12分 试题详情
 , ,
试题详情
故 为常数. ………………………………………………………………14分 为常数. ………………………………………………………………14分 试题详情
试题详情
(1)判断 在 在 上的单调性,并证明你的结论; 上的单调性,并证明你的结论; 试题详情
(2)设 ,求函数 ,求函数 的最小值. 的最小值. 试题详情
解:(1) 在 在 上为增函数…………………………………..1分 上为增函数…………………………………..1分 试题详情
∵ ,∴ ,∴ ,……….…………….3分 ,……….…………….3分 试题详情
∵ 当 时, 时, ……………………………….4分 ……………………………….4分 试题详情
∴ 当 时, 时, , , 试题详情
∴当 时, 时, ,…………………………..5分 ,…………………………..5分 试题详情
试题详情
(2)由题意及(1)可知, , , ,…………………7分 ,…………………7分 试题详情
试题详情
∵ ,∴ ,∴ ,……………..9分 ,……………..9分 试题详情
 , ,
试题详情
∴ …………………………………………………..10分 …………………………………………………..10分 试题详情
令 则 则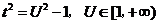 试题详情
∴ ,……………………………………………11分 ,……………………………………………11分 试题详情
∵ ………………………………..…….12分 ………………………………..…….12分 试题详情
∴ 在 在 单增,……………………………………..……………..13分 单增,……………………………………..……………..13分 试题详情
∴当 时, 时, 。………………………………………………..14分 。………………………………………………..14分 试题详情
试题详情
(1)求 的值; 的值; 试题详情
试题详情
试题详情
由题意知:当 时, 时, , , 试题详情
又∵ ∴
∴ …………………………………………….3分 …………………………………………….3分 试题详情
试题详情
试题详情
显然, 对 对 恒成立。 恒成立。 试题详情
∴ , , …………………………………………………………………….6分 …………………………………………………………………….6分 试题详情
(2)∵ , , , , 试题详情
∴ , , ……………………………..7分 ……………………………..7分 试题详情
试题详情
∴ ,………………………………………………………..…..9分 ,………………………………………………………..…..9分 试题详情
 ……………...10分 ……………...10分
试题详情
又∵ …………….12分 …………….12分 试题详情
∴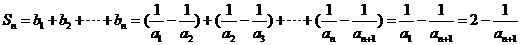
………….13分 试题详情
∴ ,∴ ,∴ 为定值。………………………..14分 为定值。………………………..14分 试题详情
| 
 (S为底面面积,h为高)
(S为底面面积,h为高)

 ,
, ={1,2,5},
={1,2,5}, ,则
,则 ∩CU
∩CU =(
B )
=(
B ) 2.已知复数
2.已知复数 ,且
,且 ,则实数a的值为(
C )
,则实数a的值为(
C ) 的最大值为4,最小值为0,最小正周期为
的最大值为4,最小值为0,最小正周期为 ,直线
,直线 是其图象的一条对称轴,则下面各式中符合条件的解析式是(
D )
是其图象的一条对称轴,则下面各式中符合条件的解析式是(
D )