科目：gzsx 来源：2012高三数学一轮复习单元练习题 函数与数列(3) 题型：044
已知函数g(x)＝
＋lnx在[1，＋∞)上为增函数，且
∈(0，π)，f(x)＝mx－
－lnx，m∈R．
(1)求的值；
(2)若F(x)＝f(x)－g(x)在[1，＋∞)上为单调函数，求m的取值范围．
科目：gzsx 来源：河南省镇平一高2012届高三下学期第三次周考数学理科试题 题型：044
已知函数
g(x)＝
＋lnx在[1，＋∞)上为增函数，且
∈(0，π)，f(x)＝mx－
－lnx，m∈R．
(Ⅰ)求的值；
(Ⅱ)若f(x)－g(x)在[1，＋∞)上为单调函数，求m的取值范围；
(Ⅲ)设h(x)＝
，若在[1，e]上至少存在一个x0，使得f(x0)－g(x0)＞h(x0)成立，求m的取值范围．
科目：gzsx 来源：江西省新余一中2012届高三第六次模拟数学文科试题 题型：044
已知函数f(x)＝ax2＋lnx(a∈R)．
(1)当a＝2时，求f(x)在区间[e，e2]上的最大值和最小值；
(2)如果函数g(x)，f1(x)，f2(x)在公共定义域D上，满足f1(x)＜g(x)＜f2(x)那么就称g(x)为f1(x)，f2(x)的“伴随函数”．已知函数f1(x)＝(a－
)x2＋2ax＋(1－a2)lnx，f2(x)＝
x2＋2ax．若在区间(1，＋∞)上，函数f(x)是f1(x)，f2(x)的“伴随函数”，求a的取值范围．
科目：gzsx 来源：浙江省浙大附中2012届高三上学期期中考试数学理科试题 题型：044
已知函数g(x)＝
＋lnx在[1，＋∞)上为增函数，且
∈(0，π)，f(x)＝mx－
－lnx，m∈R．
(1)求的值；
(2)若f(x)－g(x)在[1，＋∞)上为单调函数，求m的取值范围；
(3)设h(x)＝
，若在[1，e]上至少存在一个x0，使得f(x0)－g(x0)＞h(x0)成立，求m的取值范围．
科目：gzsx 来源：山东省日照市2012届高三第一次模拟考试数学文科试题 题型：044
已知函数f(x)＝ax2＋lnx(a∈R)．
(Ⅰ)当
时，求f(x)在区间[1，e]上的最大值和最小值；
(Ⅱ)如果在公共定义域D上的函数g(x)，f1(x)，f2(x)满足f1(x)＜g(x)＜f2(x)，那么就称g(x)为f1(x)、f2(x)的“活动函数”，已知函数f1(x)＝(a－
)x2＋2ax＋(1－a2)lnx，f2(x)＝
x2＋2ax，若在区间(1，＋∞)上，函数f(x)是f1(x)、f2(x)的“活动函数”，求实数a的取范围．
科目：gzsx 来源：浙江省浙江大学附属中学2012届高三上学期期中考试数学理科试题 题型：044
已知函数g(x)＝
＋lnx在[1，＋∞)上为增函数，且
∈(0，π)，f(x)＝mx－
－lnx，m∈R．
(1)求的值；
(2)若f(x)－g(x)在[1，＋∞)上为单调函数，求m的取值范围；
(3)设h(x)＝
，若在[1，e]上至少存在一个x0，使得f(x0)－g(x0)＞h(x0)成立，求m的取值范围．
科目：gzsx 来源： 题型：
| 1 |
| x |
| m-1 |
| x |
| 2e |
| x |
科目：gzsx 来源：2014届浙江省高二下学期期末文科数学试卷（解析版） 题型：填空题
若函数f(x)在定义域D内某区间I上是增函数，且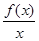
在I上是减函数，则称y＝f(x)在I 上是“弱增函数”．已知函数h(x)＝x2－(b－1)x＋b在(0，1]上是“弱增函数”，则实数b的值为 ．
科目：gzsx 来源： 题型：
已知函数g(x)＝ax3＋bx2＋cx(a∈R且a≠0)，g(－1)＝0，且g(x)的导函数f(x)满足f(0)f(1)≤0.设x1、x2为方程f(x)＝0的两根．
(1)求
的取值范围；
(2)若当|x1－x2|最小时，g(x)的极大值比极小值大
，求g(x)的解析式．
科目：gzsx 来源： 题型：
已知x>
，函数f(x)＝x2，h(x)＝2elnx(e为自然常数)．
(1)求证：f(x)≥h(x)；
(2)若f(x)≥h(x)且g(x)≤h(x)恒成立，则称函数h(x)的图像为函数f(x)，g(x)的“边界”．已知函数g(x)＝－4x2＋px＋q(p，q∈R)，试判断“函数f(x)，g(x)以函数h(x)的图像为边界”和“函数f(x)，g(x)的图像有且仅有一个公共点”这两个条件能否同时成立？若能同时成立，请求出实数p、q的值；若不能同时成立，请说明理由．
科目：gzsx 来源：2014届江苏省高一第二学期第一次月考数学试 题型：解答题
已知函数f(x)＝3x2＋bx＋c，不等式f(x)>0的解集为(－∞，－2)∪(0，＋∞)．
(1) 求函数f(x)的解析式；
(2) 已知函数g(x)＝f(x)＋mx－2在(2，＋∞)上单调增，求实数m的取值范围；
(3) 若对于任意的x∈[－2,2]，f(x)＋n≤3都成立，求实数n的最大值．
科目：gzsx 来源： 题型：
设函数f(x)＝－
x3＋x2＋(m2－1)x(x∈R)，其中m>0.
(1)当m＝1时，求曲线y＝f(x)在(1，f(1))点处的切线的方程；
(2)求函数f(x)的单调区间与极值；
(3)已知函数g(x)＝f(x)＋有三个互不相同的零点，求m的取值范围．
科目：gzsx 来源：江苏省盐城市2012届高三3月第二次模拟考试数学试题 题型：044
已知函数f1(x)＝e|x－2a+1|，f2(x)＝e|x－a|+1，x∈R．
(1)若a＝2，求f(x)＝f1(x)＋f2(x)在x∈[2，3]上的最小值；
(2)若x∈[a，＋∞)时，f2(x)≥f1(x)，求a的取值范围；
(3)求函数g(x)＝
－
在x∈[1，6]上的最小值；
科目：gzsx 来源： 题型：
已知函数f(x)＝ax2＋ln x(a∈R)
(Ⅰ)当a＝2时，求f(x)在区间[e，e2]上的最大值和最小值；
(Ⅱ)如果函数g(x)，f1(x)，f2(x)在公共定义域D上，满足f1(x)<g(x)<f2(x)，那么就称g(x)为f1(x)，f2(x)的“伴随函数”.已知函数f1(x)＝
x2＋2ax＋(1－a2)ln x，f2(x)＝
x2＋2ax.若在区间(1，＋∞)上，函数f(x)是f1(x)，f2(x)的“伴随函数”，求a的取值范围.
科目：gzsx 来源：河北省正定中学2012届高三第三次月考数学试题 题型：044
已知函数g(x)＝aex－1－x2＋bln(x＋1)，a，b∈R
(Ⅰ)若a＝0，b＝1，求函数g(x)的单调区间；
(Ⅱ)若f(x)的图象在(0，g(0))处与直线x－ey＋1＝0相切，
(ⅰ)求a、b的值；
(ⅱ)求证：
，
．
科目：gzsx 来源：2008年普通高等学校招生全国统一考试(江西卷)、数学(理) 题型：044
已知函数
，x∈(0，＋∞)．
(1)当a＝8时，求f(x)的单调区间；
(2)对任意正数a，证明：1＜f(x)＜2．
科目：gzsx 来源：福建师大附中2010－2011学年高二下学期期中考试数学理科试题 题型：044
已知函数
在x＝2取得极值．
(Ⅰ)确定a的值并求函数的单调区间；
(Ⅱ)若关于x的方程f(x)＝b至多有两个零点，求实数b的取值范围．
科目：gzsx 来源：安徽省马鞍山二中2011－2012学年高二下学期期中素质测试数学文科试题 题型：044
已知函数t(x)＝x3＋mx2＋x是奇函数，s(x)＝ax2＋nx＋2是偶函数，设
f(x)＝t(x)＋s(x)．
(1)若a＝－1，令函数g(x)＝2x－f(x)，求函数g(x)在(－1，2)上的极值；
(2)对
恒有
成立，求实数a的取值范围．
科目：gzsx 来源：东北四校2012届高三第一次高考模拟考试数学理科试题 题型：044
已知函数
在x＝1处取得极值为2，设函数y＝f(x)图象上任意一点(x0，f(x0))处的切线斜率为k．
(1)求k的取值范围；
(2)若对于任意0＜x1＜x2＜1，存在k，使得
，求证：x1＜|x0|＜x2．
科目：gzsx 来源：2009-2010学年江西省上饶市广丰中学高三（上）第二次段考数学试卷（理科）（解析版） 题型：解答题
；
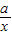