练习册

  • 练习册
  • 试题
    精英家教网 > 试题搜索列表 >已知椭圆：x2a2+y2b2=1（a＞b

    已知椭圆：x2a2+y2b2=1（a＞b答案解析

    科目：gzsx 来源： 题型：

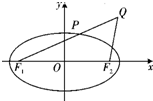    （2012•武汉模拟）如图，已知椭圆Γ：
    x2
    a2
    +
    y2
    b2
    =1（a＞b＞0）的左、右焦点分别是F1（-c，0）、F2（c，0），Q是椭圆外的一个动点，满足|F1Q|=2a．点P是线段F1Q与该椭圆的交点，点M在线段F2Q上，且满足
    PM
    •
    MF2
    =0，|
    MF2
    |≠0．
    （Ⅰ）求点M的轨迹C的方程；
    （Ⅱ）设不过原点O的直线l与轨迹C交于A，B两点，若直线OA，AB，OB的斜率依次成等比数列，求△OAB面积的取值范围；
    （Ⅲ）由（Ⅱ）求解的结果，试对椭圆Γ写出类似的命题．（只需写出类似的命题，不必说明理由）

    查看答案和解析>>

    科目：gzsx 来源： 题型：

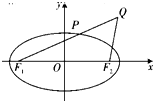    如图，已知椭圆Γ：
    x2
    a2
    +
    y2
    b2
    =1    （a＞b＞0）的左、右焦点分别是F1（-c，0）、F2（c，0），Q是椭圆外的一个动点，满足|
    F1Q
    |=2a．点P是线段F1Q与该椭圆的交点，点M在线段F2Q上，且满足
    PM
    •
    MF1
    =0，|
    MF2
    |≠0．
    （Ⅰ）求点M的轨迹C的方程；
    （Ⅱ）设不过原点O的直线l与轨迹C交于A，B两点，若直线OA，AB，OB的斜率依次成等比数列，求△OAB面积的取值范围．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    （2012•武汉模拟）已知椭圆Γ：
    x2
    a2
    +
    y2
    b2
    =1（a＞b＞0）的离心率为
    2
    3
    ，半焦距为c（c＞0），且a-c=1．经过椭圆的左焦点F，斜率为k1（k1≠0）的直线与椭圆交于A，B两点，O为坐标原点．
    （Ⅰ）求椭圆Γ的标准方程；
    （Ⅱ）当k1=1时，求S△AOB的值；
    （Ⅲ）设R（1，0），延长AR，BR分别与椭圆交于C，D两点，直线CD的斜率为k2，求证：
    k1
    k2
    为定值．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    如图，已知半径为r的圆M的内接四边形ABCD的对角线AC和BD相互垂直且交点为P．
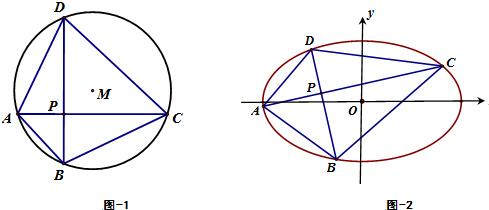
    精英家教网
    （1）若四边形ABCD中的一条对角线AC的长度为d（0＜d＜2r），试求：四边形ABCD面积的最大值；
    （2）试探究：当点P运动到什么位置时，四边形ABCD的面积取得最大值，最大值为多少？
    （3）对于之前小题的研究结论，我们可以将其类比到椭圆的情形．如图2，设平面直角坐标系中，已知椭圆Γ：
    x2
    a2
    +
    y2
    b2
    =1    （a＞b＞0）的内接四边形ABCD的对角线AC和BD相互垂直且交于点P．试提出一个由类比获得的猜想，并尝试给予证明或反例否定．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    （2013•合肥二模）已知椭圆：
    x2
    a2
    +
    y2
    b2
    =1（a＞b＞0）的长轴长为4，且过点（
    		3
    ，
    1
    2
    ）．
    （Ⅰ）求椭圆的方程；
    （Ⅱ）设A，B，M是椭圆上的三点．若
    OM
    =
    3
    5
    OA
    +
    4
    5
    OB
    ，点N为线段AB的中点，C（-
    		6
    2
    ，0），D（
    		6
    2
    ，0），求证：|NC|+|ND|=2
    		2
    ．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    （2013•宁德模拟）已知椭圆Γ：
    x2
    a2
    +
    y2
    b2
    =1    （a＞b＞0）过点A（0，2），离心率为
    		2
    2
    ，过点A的直线l与椭圆交于另一点M．
    （I）求椭圆Γ的方程；
    （II）是否存在直线l，使得以AM为直径的圆C，经过椭圆Γ的右焦点F且与直线 x-2y-2=0相切？若存在，求出直线l的方程；若不存在，请说明理由．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知椭圆：
    x2
    a2
    +
    y2
    b2
    =1    （a＞b＞0）的左、右焦点分别为F1、F2，以F1为顶点，F2为焦点的抛物线经过椭圆短轴的两端点，则a：b=
    3：2
    		2
    3：2
    		2
    ．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    （2010•江苏模拟）已知椭圆方程
    x2
    a2
    +
    y2
    b2
    =1    （a＞b＞0），当a2+
    16
    b(a-b)
    的最小值时，椭圆的离心率e=
    		3
    2
    		3
    2
    ．

    查看答案和解析>>

    科目：gzsx 来源：武汉模拟 题型：解答题

    已知椭圆Γ：
    x2
    a2
    +
    y2
    b2
    =1（a＞b＞0）的离心率为
    2
    3
    ，半焦距为c（c＞0），且a-c=1．经过椭圆的左焦点F，斜率为k1（k1≠0）的直线与椭圆交于A，B两点，O为坐标原点．
    （Ⅰ）求椭圆Γ的标准方程；
    （Ⅱ）当k1=1时，求S△AOB的值；
    （Ⅲ）设R（1，0），延长AR，BR分别与椭圆交于C，D两点，直线CD的斜率为k2，求证：
    k1
    k2
    为定值．

    查看答案和解析>>

    科目：gzsx 来源：不详 题型：填空题

    已知椭圆：
    x2
    a2
    +
    y2
    b2
    =1    （a＞b＞0）的左、右焦点分别为F1、F2，以F1为顶点，F2为焦点的抛物线经过椭圆短轴的两端点，则a：b=______．

    查看答案和解析>>

    科目：gzsx 来源：宁德模拟 题型：解答题

    已知椭圆Γ：
    x2
    a2
    +
    y2
    b2
    =1    （a＞b＞0）过点A（0，2），离心率为
    		2
    2
    ，过点A的直线l与椭圆交于另一点M．
    （I）求椭圆Γ的方程；
    （II）是否存在直线l，使得以AM为直径的圆C，经过椭圆Γ的右焦点F且与直线 x-2y-2=0相切？若存在，求出直线l的方程；若不存在，请说明理由．

    查看答案和解析>>

    科目：gzsx 来源：不详 题型：解答题

    已知椭圆：
    x2
    a2
    +
    y2
    b2
    =1（a＞b＞0）的长轴长为4，且过点（
    		3
    ，
    1
    2
    ）．
    （I）求椭圆的方程；
    （II）设A，B，M是椭圆上的三点．若
    OM
    =
    3
    5
    OA
    +
    4
    5
    OB
    ，点N为线段AB的中点，C（-
    		6
    2
    ，0），D（
    		6
    2
    ，0），求证：|NC|+|ND|=2
    		2
    ．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    定义：离心率e=
    		5
    -1
    2
    的椭圆为“黄金椭圆”，已知E：
    x2
    a2
    +
    y2
    b2
    =1    （a＞b＞0）的一个焦点为F（c，0）（c＞0），则E为“黄金椭圆”是a，b，c成等比数列的（　　）

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    （2013•红桥区二模）已知椭圆：
    x2
    a2
    +
    y2
    b2
    =l（a＞b＞0）的一个顶点坐标为B（0，1），若该椭圆的离心率等于
    		3
    2
    ．
    （1）求椭圆的方程．
    （2）Q是椭圆上位于x轴下方的一点，F1F2分别是椭圆的左、右焦点，直线QF1的倾斜角为
    π
    6
    ，求△QF1F2的面积；
    （3）以B为直角顶点作椭圆的内接等腰直角三角形ABC，判断这样的三角形存在吗？若存在，有几个？若不存在，请说明理由．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    （2013•红桥区二模）已知椭圆：
    x2
    a2
    +
    y2
    b2
    =l（a＞b＞0）的一个顶点坐标为B（0，1），若该椭圆的离心率等于
    		3
    2
    ．
    （1）求椭圆的方程．
    （2）设Q是椭圆上任意一点，F1F2分别是左、右焦点，求∠F1QF2的取值范围；
    （3）以B为直角顶点作椭圆的内接等腰直角三角形ABC，判断这样的三角形存在吗？若存在，有几个？若不存在，请说明理由．

    查看答案和解析>>

    科目：gzsx 来源：红桥区二模 题型：解答题

    已知椭圆：
    x2
    a2
    +
    y2
    b2
    =l（a＞b＞0）的一个顶点坐标为B（0，1），若该椭圆的离心率等于
    		3
    2
    ．
    （1）求椭圆的方程．
    （2）Q是椭圆上位于x轴下方的一点，F1F2分别是椭圆的左、右焦点，直线QF1的倾斜角为
    π
    6
    ，求△QF1F2的面积；
    （3）以B为直角顶点作椭圆的内接等腰直角三角形ABC，判断这样的三角形存在吗？若存在，有几个？若不存在，请说明理由．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知双曲线方程
    x2
    a2
    -
    y2
    b2
    =1（a＞b＞0），过右焦点F2且倾斜角为60°的线段F2M与y轴交于M，与双曲线交于N，已知
    MF2
    =4
    NF2
    ，则该双曲线的离心率为（　　）
    A、
    		13
    -1
    3
    B、
    		13
    -1
    C、
    		13+1
    3
    D、
    		13
    +1

    查看答案和解析>>

    科目：gzsx 来源：不详 题型：单选题

    已知双曲线方程
    x2
    a2
    -
    y2
    b2
    =1（a＞b＞0），过右焦点F2且倾斜角为60°的线段F2M与y轴交于M，与双曲线交于N，已知
    MF2
    =4
    NF2
    ，则该双曲线的离心率为（　　）
    A．
    		13
    -1
    3
    		B．
    		13
    -1    		C．
    		13+1
    3
    		D．
    		13
    +1

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知椭圆Γ：
    x2
    a2
    +
    y2
    b2
    =1(a＞b＞0)    的左、右焦点为F1、F2，过点F1斜率为正数的直线交Γ与A、B两点，且AB⊥AF2，|AF2|、|AB|、|BF2|成等差数列．
    （Ⅰ）求Γ的离心率；
    （Ⅱ）若直线y=kx（k＜0）与Γ交于C、D两点，求使四边形ABCD面积S最大时k的值．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    （2013•武汉模拟）过椭圆Γ：
    x2
    a2
    +
    y2
    b2
    =1（a＞b＞0）右焦点F2的直线交椭圆于A，B两点，F1为其左焦点，已知△AF1B的周长为8，椭圆的离心率为
    		3
    2
    ．
    （Ⅰ）求椭圆Γ的方程；
    （Ⅱ）是否存在圆心在原点的圆，使得该圆的任意一条切线与椭圆Γ恒有两个交点P，Q，且
    OP
    ⊥
    OQ
    ？若存在，求出该圆的方程；若不存在，请说明理由．

    查看答案和解析>>