
3、“诱”
遇到有逆反心理的同学,还得尝试“诱惑”法吸引他们去读书。我常用的方法有两招:
A、开展课前5分钟名著赏析活动。先由老师带头读或说一段,然后启发学生自己鉴赏,最后老师总结归纳。比如,先欣赏《水浒传》里“鲁提辖拳打镇关西”中的繁笔描写,再诱惑学生读“林教头风雪山神庙”一节中的简笔描写,使学生对名著作者产生崇拜心理,接着读下去也就成了可能。
B、在对课本进行拓展延伸的时候,有意的在课堂上讲一些与教学内容相关联的名著内容或精彩片段,在学生听得入神时突然打住,说是时间关系暂时不说了,若你们着急,先抽时间读一下过过眼瘾,有机会咱们再一块切磋。也许一次两次不管用,但次数多了,学生自然就有耐不住性子的了。只要他们主动打开书,就不愁他们不去读!
1、“逼”
向学生推荐教育部规定的中学生必须读或应该读的中外名著,强调读名著的种种好处,并硬性规定每人每学期必须读2-3本名著,学期末开展读名著交流活动,每人都要发言。落实到每周,要求每周要摘抄2页笔记,并作出100字左右的点评。老师每两周一检查,一评比。
 b)∈M,且对M中的其它元素(c,d),总有c≥a,则a=____.
b)∈M,且对M中的其它元素(c,d),总有c≥a,则a=____.
分析:读懂并能揭示问题中的数学实质,将是解决该问题的突破口.怎样理解“对M中的其它元素(c,d),总有c≥a”?M中的元素又有什么特点?
解:依题可知,本题等价于求函数x=f(y)=(y+3)·|y-1|+(y+3)







(2)当1≤y≤3时,

所以当y=1时, = 4.
= 4.


简评:题设条件中出现集合的形式,因此要认清集合元素的本质属性,然后结合条件,揭示
其数学实质.即求集合M中的元素满足关系式


例2.已知非负实数 ,
, 满足
满足 且
且 ,则
,则 的最大值是( )
的最大值是( )

A.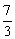 B.
B. C.
C. D.
D. 

解:画出图象,由线性规划知识可得,选D
例3.数列 由下列条件确定:
由下列条件确定:

(1)证明:对于 ,
,
(2)证明:对于 .
.
证明:(1)



(2)当 时,
时,

= .
.
例4.解关于 的不等式:
的不等式:

分析:本例主要复习含绝对值不等式的解法,分类讨论的思想。本题的关键不是对参数 进行讨论,而是去绝对值时必须对末知数进行讨论,得到两个不等式组,最后对两个不等式组的解集求并集,得出原不等式的解集.
进行讨论,而是去绝对值时必须对末知数进行讨论,得到两个不等式组,最后对两个不等式组的解集求并集,得出原不等式的解集.
解:当





 .
.
例5.若二次函数y=f(x)的图象经过原点,且1≤f(-1)≤2,3≤f(1)≤4,求f(-2)的范围.
分析:要求f(-2)的取值范围,只需找到含人f(-2)的不等式(组).由于y=f(x)是二次函数,所以应先将f(x)的表达形式写出来.即可求得f(-2)的表达式,然后依题设条件列出含有f(-2)的不等式(组),即可求解.
解:因为y=f(x)的图象经过原点,所以可设y=f(x)=ax2+bx.于是


解法一(利用基本不等式的性质)
不等式组(Ⅰ)变形得


 (Ⅰ)
(Ⅰ)
所以f(-2)的取值范围是[6,10].
解法二(数形结合)


建立直角坐标系aob,作出不等式组(Ⅰ)所表示的区域,如图6中的阴影部分.因为f(-2)=4a-2b,所以4a-2b-f(-2)=0表示斜率为2的直线系.如图6,当直线4a-2b-f(-2)=0过点A(2,1),B(3,1)时,分别取得f(-2)的最小值6,最大值10.即f(-2)的取值范围是:6≤f(-2)≤10.
解法三(利用方程的思想)


又f(-2)=4a-2b=3f(-1)+f(1),而
1≤f(-1)≤2,3≤f(1)≤4, ①
所以 3≤3f(-1)≤6. ②
①+②得4≤3f(-1)+f(1)≤10,即6≤f(-2)≤10.
简评:(1)在解不等式时,要求作同解变形.要避免出现以下一种错解:
 2b,8≤4a≤12,-3≤-2b≤-1,所以 5≤f(-2)≤11.
2b,8≤4a≤12,-3≤-2b≤-1,所以 5≤f(-2)≤11.
(2)对这类问题的求解关键一步是,找到f(-2)的数学结构,然后依其数学结构特征,揭示其代数的、几何的本质,利用不等式的基本性质、数形结合、方程等数学思想方法,从不同角度去解决同一问题.若长期这样思考问题,数学的素养一定会迅速提高.
例6.设函数f(x)=ax2+bx+c的图象与两直线y=x,y= x,均不相交.试证明对一切
x,均不相交.试证明对一切 都有
都有 .
.
分析:因为x∈R,故|f(x)|的最小值若存在,则最小值由顶点确定,故设f(x)=a(x-x0)2+f(x0).
证明:由题意知,a≠0.设f(x)=a(x-x0)2+f(x0),则

又二次方程ax2+bx+c=±x无实根,故
Δ1=(b+1)2-4ac<0,Δ2=(b-1)2-4ac<0.
所以(b+1)2+(b-1)2-8ac<0,即2b2+2-8ac<0,即b2-4ac<-1,所以|b2-4ac|>1.






简评:从上述几个例子可以看出,在证明与二次函数有关的不等式问题时,如果针对题设条件,合理采取二次函数的不同形式,那么我们就找到了一种有效的证明途径.
例7.某城市2001年末汽车保有量为30万辆,预计此后每年报废上一年末汽车保有量的6%,并且每年新增汽车数量相同.为了保护城市环境,要求该城市汽车保有量不超过60万辆,那么每年新增汽车数量不应超过多少辆?
解:设2001年末的汽车保有量为 ,以后每年末的汽车保有量依次为
,以后每年末的汽车保有量依次为 ,每年新增汽车
,每年新增汽车 万辆.由题意得
万辆.由题意得


4.根据题目结构特点,执果索因,往往是有效的思维方法.
3.不等式证明方法有多种,既要注意到各种证法的适用范围,又要注意在掌握常规证法的基础上,选用一些特殊技巧。如运用放缩法证明不等式时要注意调整放缩的度.
2.解含参数不等式时,要特别注意数形结合思想,函数与方程思想,分类讨论思想的录活运用.
1.解不等式的基本思想是转化、化归,一般都转化为最简单的一元一次不等式(组)或一元二次不等式(组)来求解.
7.通过不等式的基本知识、基本方法在代数、三角函数、数列、复数、立体几何、解析几何等各部分知识中的应用,深化数学知识间的融汇贯通,从而提高分析问题解决问题的能力.在应用不等式的基本知识、方法、思想解决问题的过程中,提高学生数学素质及创新意识.
6.不等式应用问题体现了一定的综合性.这类问题大致可以分为两类:一类是建立不等式、解不等式;另一类是建立函数式求最大值或最小值.利用平均值不等式求函数的最值时,要特别注意“正数、定值和相等”三个条件缺一不可,有时需要适当拼凑,使之符合这三个条件.利用不等式解应用题的基本步骤:1.审题,2.建立不等式模型,3.解数学问题,4.作答.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com