
同步练习 9.1平面的性质与直线的位置关系
[选择题]
1.下列四个命题:
(1)分别在两个平面内的两条直线是异面直线
(2)和两条异面直线都垂直的直线有且只有一条
(3)和两条异面直线都相交的两条直线必异面
(4)若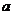 与
与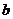 是异面直线,
是异面直线,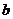 与
与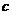 是异面直线,则
是异面直线,则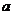 与
与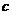 也异面
也异面
其中真命题个数为 ( )
A.3 B.2 C.1 D.0
[例1]用图形表示:a∩b=m,aÌa,bÌb,a∩m=A,b∩m=B,c∩a=P,PÏa,cËb.
图略
思悟提炼:熟悉图形语言、符号语言之间的互化.提高画图能力.
[例2]P是正方体ABCD-A1B1C1D1上一点,(不是端点),求证:过P点有且只有一条直线与直线BC、C1D1相交.
证明:依题设,平面BCP与直线C1D1
有且只有一个交点,设为Q,过两点Q、P有且只有一条直线,且与BC必相交.
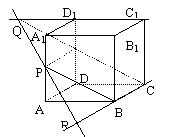

思悟提炼:1.线面相交,有且只有一个交点.一个平面内的直线不平行就相交.
[例3](1)三条直线a,b,c互相平行,且都与直线m相交,求证:这四条直线共面;
(2)在正方体ABCD-A1B1C1D1中,M,N,P,Q,R,S是棱的中点,
求证:MNPQRS是正六边形.
证明:
(1)设a,m确定平面α再证b, c在α内.
(2)证SR//MQ//NP,且都与RN相交.
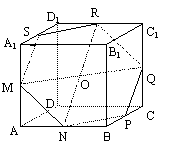

思悟提炼:证明点或线共面的方法:--
[例4]如图,已知DABC和DA¢B¢C¢不共面,直线AA¢、BB¢、CC¢两两相交.
(1)求证:这三条直线AA¢、BB¢、CC¢交于一点;
(2) 若直线AB和A¢B¢、BC和B¢C¢、CA和C¢A¢分别交于P、Q、R,求证:P、Q、R三点共线.
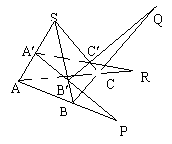

思悟提炼:用平面的基本性质证明空间三点共线、三线共点的方法.
[例5] 长方体ABCD-A1B1C1D1中,已知AB=a,BC=b,AA1=c,且a>b,求:
(1) 下列异面直线之间的距离:
AB与CC1;AB与A1C1;AB与B1C.
(2)异面直线D1B与AC所成角的余弦值.
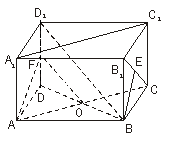

解(1):BC为异面直线AB与CC1的公垂线段,故AB与CC1的距离为b.
AA1为异面直线AB与A1C1的公垂线段,故AB与A1C1的距离为c.
过B作BE⊥B1C,垂足为E,则BE为异面直线AB与B1C的公垂线,BE=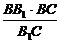 =
=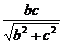 ,即为所求.
,即为所求.
(2)解法一:连结BD交AC于点O,取DD1的中点F,连结OF、AF,则OF∥D1B,∴∠AOF就是异面直线D1B与AC所成的角.
∵ AO=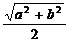 ,OF=
,OF=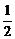
BD1=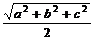 ,AF=
,AF=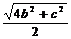 ,
,
∴ 在△AOF中,
cos∠AOF=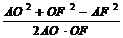
=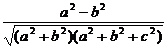
解法二:补图形如下,在ΔBGD1中,∠GBD1为所求角的补角--

3.C; 4.C 5.C
2. ´;Ö;Ö;´;Ö;´;´;´.
1.不共线;六个; 0个、一个或三个.
6.画出上题图B中平面PQR与下底面的交线.
◆答案提示:
5.下列各图是正方体或正四面体,P、Q、R、S分别是所在棱的中点,则PQ与SR一定是异面直线的是
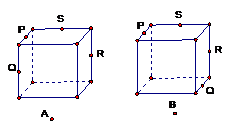
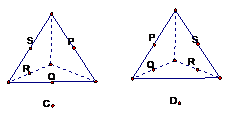
4. 直线a、b相交于点O且a、b成60°角,过点O与a、b都成60°角的直线有( )
A.1条 B.2条 C.3条 D.4条
3.(2006福建)对平面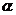 和共面的直线
和共面的直线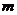 、
、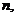 下列命题中真命题是
( )
下列命题中真命题是
( )
(A)若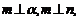 则
则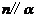
(B)若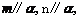 则
则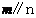
(C)若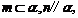 则
则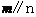
(D)若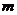 、
、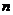 与
与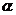 所成的角相等,则
所成的角相等,则
2. 判断下列命题真假
(1)四边相等且有一个内角是直角的四边形是正方形; ( )
(2)四点不共面,则其中任意三点不共线; ( )
(3)“平面不经过直线”的等价说法是“直线上至多有一个点在平面内” ( )
(4)两个平面有三个共公点,那么这两个平面重合; ( )
(5)三个平面可以把空间分成四、六、七、八个部分; ( )
(6)过直线外一点向直线引垂线,有且只有一条; ( )
(7)异面直线a与c、b与c所成的角相等,则a与b平行或异面 ( )
(8)过空间任一点一定可以作一条直线与两条异面直线都相交. ( )
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com