
1.除去铜粉中混有少量的氧化铜,其主要操作过程是( )
A.在空气中燃烧 B.加适量稀硫酸、微热、过滤
C.加适量水、微热、过滤 D.加适量稀硫酸、微热、蒸发
例1.不用其它试剂鉴别①Na2CO3②KCl③Zn(NO3)2④CuSO4四种溶液,先直接鉴别出一种,再逐一鉴别出其余物质,则鉴别的正确顺序是( )
A. ①④③② B.④①③② C.④②①③ D.①③④②
解析:考查学生根据特征颜色,再根据鉴别物质与其它物质反应中特征,正确分析。
例2.水煤气的主要成分是H2、CO、N2、CO2和水蒸气,把该混合气体依次通入足量的烧碱溶液,灼热的氧化铜,澄清的石灰水和浓硫酸,最后剩余的气体是____.
解析:考查学生利用物质之间相互反应及其特性而除掉气体。
例3.为了除去下列物质中的杂质,试从A、B、C中选择所加试剂,再从①②③中选择操作方法,把正确序号填在空格内.
所加试剂:A.盐酸 B.硝酸银溶液 C.水
操作方法:①过滤 ②过滤、蒸发 ③过滤、洗涤
|
物质 |
杂质 |
除杂质应加的试剂 |
|
KNO3溶液 |
KCl溶液 |
|
|
Cu |
CuO |
|
解析:考查根据化学反应原理来选择除杂质的试剂和操作方法。
例4.硝酸钠溶液中含有Cu(NO3)2、AgNO3、Ba(NO3)2三种杂质,为使三种物质转化为沉淀分离出来,提供的试剂是Na2CO3溶液、NaCl溶液、NaOH溶液.若要求每次只加一种试剂,滤出一种沉淀,那么所加试剂顺序是①____②____③____
解析:考查常见物质溶解性及复分解反应条件应用。
例5.现有盐酸、氢氧化钙、碳酸钠三种溶液,请你从中选择两种溶液,用化学方法进行鉴别.要求:①选择试剂时,同类物质在鉴别中只能使用一次;②每次鉴别一步完成;③有微溶物生成的不按沉淀处理.请回答:
(1)你认为鉴别方法最多的两种溶液是:____.
(2)鉴别上述两种溶液,你所选择的试剂分别是:____.
(3)填写用上述任意一种试剂鉴别这两种溶液的实验报告:
|
实验步骤 |
实验现象 |
实验结论 |
|
|
|
|
解析:考查酸、碱、盐化学性质及其应用。
2. 在混合物分离和提纯中,记住常见物质的溶解性,强化溶解、过滤、蒸发等操作.并对复分解反应条件加深理解和应用;
1. 重点掌握常见气体:O2、H2、CO2、CO等和常见离子:H+、OH-、SO42-、Cl-、CO32-
等的鉴定方法;
4.函数定义域为 ,当
,当 时,
时,
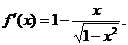
令 ,解得
,解得 ,∴
,∴ ,
,
又 ,∴
,∴
说明:对于闭区间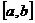 上的连续函数,如果在相应开区间
上的连续函数,如果在相应开区间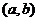 内可导,求
内可导,求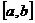 上最值可简化过程,即直接将极值点与端点的函数值比较,即可判定最大(或最小)的函数值,就是最大(或最小)值.解决这类问题,运算欠准确是普遍存在的一个突出问题,反映出运算能力上的差距.运算的准确要依靠运算方法的合理与简捷,需要有效的检验手段,只有全方位的“综合治理”才能在坚实的基础上形成运算能力,解决运算不准确的弊病.
上最值可简化过程,即直接将极值点与端点的函数值比较,即可判定最大(或最小)的函数值,就是最大(或最小)值.解决这类问题,运算欠准确是普遍存在的一个突出问题,反映出运算能力上的差距.运算的准确要依靠运算方法的合理与简捷,需要有效的检验手段,只有全方位的“综合治理”才能在坚实的基础上形成运算能力,解决运算不准确的弊病.
求两变量乘积的最大值
例 已知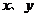 为正实数,且满足关系式
为正实数,且满足关系式 ,求
,求 的最大值.
的最大值.
分析:题中有两个变量x和y,首先应选择一个主要变量,将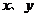 表示为某一变量(x或y或其它变量)的函数关系,实现问题的转化,同时根据题设条件确定变量的取值范围,再利用导数(或均值不等式等)求函数的最大值.
表示为某一变量(x或y或其它变量)的函数关系,实现问题的转化,同时根据题设条件确定变量的取值范围,再利用导数(或均值不等式等)求函数的最大值.
解:解法一: ,
,
∴ .
.
由 解得
解得 .
.
设
当 时,
时,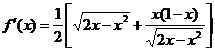
 .
.
令 ,得
,得 或
或 (舍).
(舍).
∴ ,又
,又 ,∴函数
,∴函数 的最大值为
的最大值为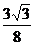 .
.
即 的最大值为
的最大值为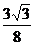 .
.
解法二:由 得
得 ,
,
设 ,
,
∴ ,设
,设 ,
,
则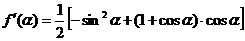

令 ,得
,得 或
或 .
.
 ,此时
,此时
∴
即当 时,
时,
说明:进行一题多解训练,是一种打开思路,激发思维,巩固基础,沟通联系的重要途径,但要明确解决问题的策略、指向和思考方法,需要抓住问题的本质,领悟真谛,巧施转化,方可快捷地与熟悉的问题接轨,在实现转化的过程中,关键是要注意变量的取值范围必须满足题设条件,以免解题陷于困境,功亏一篑.
3. .
.
令 ,即
,即 ,解得
,解得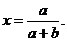
当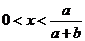 时,
时, ,当
,当 时,
时, .
.
∴函数 在点
在点 处取得极小值,也是最小值为
处取得极小值,也是最小值为
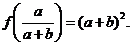 即
即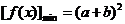 .
.
2.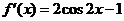 ,令
,令 ,得
,得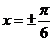 ,
,
∴ ,
,
又 .
.
∴
4.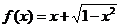 .
.
分析:函数 在给定区间上连续可导,必有最大值和最小值,因此,在求闭区间
在给定区间上连续可导,必有最大值和最小值,因此,在求闭区间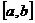 上函数的最值时,只需求出函数
上函数的最值时,只需求出函数 在开区间
在开区间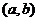 内的极值,然后与端点处函数值进行比较即可.
内的极值,然后与端点处函数值进行比较即可.
解:1.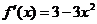 ,令
,令 ,得
,得 ,
,
∴ .又
.又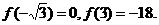
∴
3.
2. ;
;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com