
21.(2009江西卷文)数列 的通项
的通项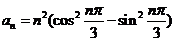 ,其前n项和为
,其前n项和为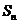 .
.
(1) 求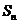 ;
;
(2)  求数列{
求数列{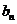 }的前n项和
}的前n项和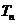 .
.
解: (1) 由于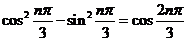 ,故
,故
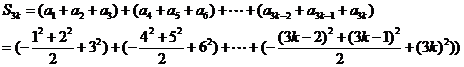
 ,
,
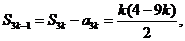

故 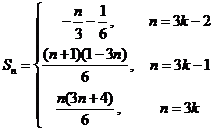 (
(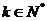 )
)
(2) 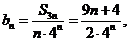


两式相减得
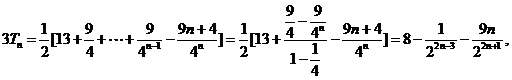
故 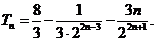
20.(2009安徽卷文)已知数列{ } 的前n项和
} 的前n项和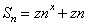 ,数列{
,数列{ }的前n项和
}的前n项和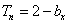
(Ⅰ)求数列{ }与{
}与{ }的通项公式;
}的通项公式;
(Ⅱ)设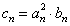 ,证明:当且仅当n≥3时,
,证明:当且仅当n≥3时, <
<


[思路]由 可求出
可求出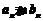 ,这是数列中求通项的常用方法之一,在求出
,这是数列中求通项的常用方法之一,在求出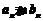 后,进而得到
后,进而得到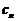 ,接下来用作差法来比较大小,这也是一常用方法。
,接下来用作差法来比较大小,这也是一常用方法。
[解析](1)由于
当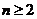 时,
时, 
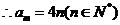
又当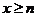 时
时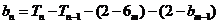

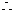 数列
数列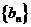 项与等比数列,其首项为1,公比为
项与等比数列,其首项为1,公比为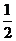
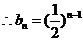


(2)由(1)知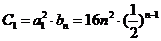
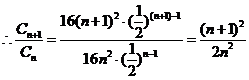
由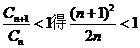 即
即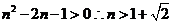 即
即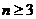
又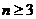 时
时 成立,即
成立,即 由于
由于 恒成立.
恒成立. 

因此,当且仅当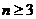 时,
时, 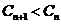
19.(2009全国卷Ⅱ文)已知等差数列{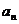 }中,
}中,
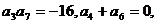 求{
求{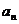 }前n项和
}前n项和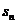 .
. 

解析:本题考查等差数列的基本性质及求和公式运用能力,利用方程的思想可求解。
解:设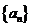 的公差为
的公差为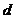 ,则
,则 

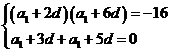
即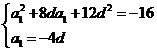
解得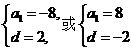
因此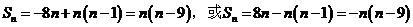
18.(2009山东卷文)等比数列{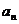 }的前n项和为
}的前n项和为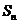 ,
已知对任意的
,
已知对任意的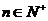 ,点
,点 ,均在函数
,均在函数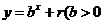 且
且 均为常数)的图像上.
均为常数)的图像上. 

(1)求r的值;
(11)当b=2时,记 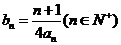 求数列
求数列 的前
的前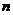 项和
项和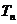
解:因为对任意的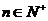 ,点
,点 ,均在函数
,均在函数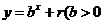 且
且 均为常数)的图像上.所以得
均为常数)的图像上.所以得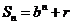 ,
,
当 时,
时, ,
, 

当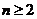 时,
时,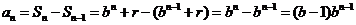 ,
,
又因为{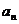 }为等比数列, 所以
}为等比数列, 所以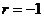 , 公比为
, 公比为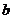 , 所以
, 所以
(2)当b=2时,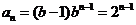 ,
, 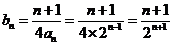
则
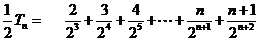


相减,得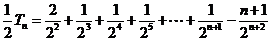


所以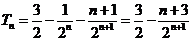
[命题立意]:本题主要考查了等比数列的定义,通项公式,以及已知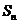 求
求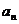 的基本题型,并运用错位相减法求出一等比数列与一等差数列对应项乘积所得新数列的前
的基本题型,并运用错位相减法求出一等比数列与一等差数列对应项乘积所得新数列的前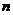 项和
项和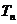 .
.
17.(2009北京文)设数列 的通项公式为
的通项公式为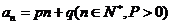 . 数列
. 数列 定义如下:对于正整数m,
定义如下:对于正整数m,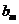 是使得不等式
是使得不等式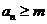 成立的所有n中的最小值.
成立的所有n中的最小值.
(Ⅰ)若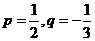 ,求
,求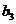 ;
;
(Ⅱ)若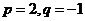 ,求数列
,求数列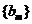 的前2m项和公式;
的前2m项和公式;
(Ⅲ)是否存在p和q,使得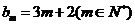 ?如果存在,求p和q的取值范围;如果不存在,请说明理由.
?如果存在,求p和q的取值范围;如果不存在,请说明理由.
[解析]本题主要考查数列的概念、数列的基本性质,考查运算能力、推理论证能力、
分类讨论等数学思想方法.本题是数列与不等式综合的较难层次题.
解(Ⅰ)由题意,得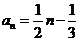 ,解
,解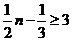 ,得
,得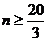 .
. 

∴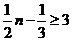 成立的所有n中的最小整数为7,即
成立的所有n中的最小整数为7,即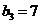 .
.
(Ⅱ)由题意,得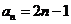 ,
,
对于正整数,由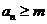 ,得
,得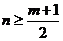 .
.
根据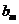 的定义可知
的定义可知
当 时,
时,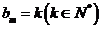 ;当
;当 时,
时,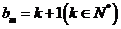 .
.
∴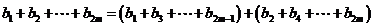
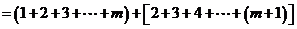
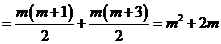 .
.
(Ⅲ)假设存在p和q满足条件,由不等式 及
及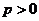 得
得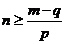 .
.
∵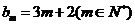 ,根据
,根据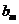 的定义可知,对于任意的正整数m 都有
的定义可知,对于任意的正整数m 都有
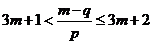 ,即
,即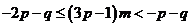 对任意的正整数m都成立.
对任意的正整数m都成立.
当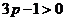 (或
(或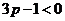 )时,得
)时,得 (或
(或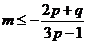 ),
),
这与上述结论矛盾!
当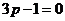 ,即
,即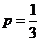 时,得
时,得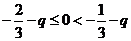 ,解得
,解得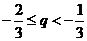 .
.
∴ 存在p和q,使得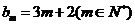 ;
;
p和q的取值范围分别是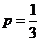 ,
,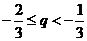 ..
..
16.(2009浙江文)设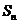 为数列
为数列 的前
的前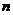 项和,
项和, ,
,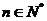 ,其中
,其中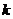 是常数.
是常数.
(I) 求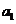 及
及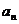 ;
;
(II)若对于任意的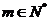 ,
, ,
,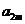 ,
,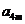 成等比数列,求
成等比数列,求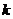 的值.
的值.
解(Ⅰ)当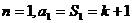 ,
,
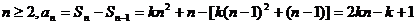 (
(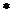 )
)
经验, (
(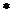 )式成立,
)式成立,
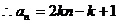
(Ⅱ)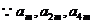 成等比数列,
成等比数列,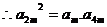 ,
,
即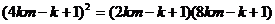 ,整理得:
,整理得: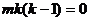 ,
,
对任意的 成立,
成立,
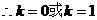
15.(2009辽宁卷理)等差数列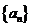 的前
的前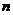 项和为
项和为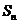 ,且
,且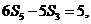 则
则
解析 ∵Sn=na1+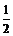 n(n-1)d
n(n-1)d 

∴S5=5a1+10d,S3=3a1+3d
∴6S5-5S3=30a1+60d-(15a1+15d)=15a1+45d=15(a1+3d)=15a4
答案 
三、解答题
14.(2009全国卷Ⅱ理)设等差数列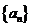 的前
的前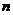 项和为
项和为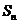 ,若
,若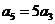 则
则
解析 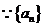 为等差数列,
为等差数列,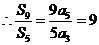
答案 9
13.(2009全国卷Ⅱ文)设等比数列{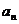 }的前n项和为
}的前n项和为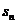 。若
。若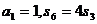 ,则
,则 =
×
=
×
答案:3
解析:本题考查等比数列的性质及求和运算,由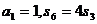 得q3=3故a4=a1q3=3
得q3=3故a4=a1q3=3
12.(2009北京文)若数列 满足:
满足: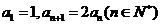 ,则
,则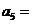 ;前8项的和
;前8项的和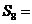 .(用数字作答)
.(用数字作答)
答案 225
.解析 本题主要考查简单的递推数列以及数列的求和问题. 属于基础知识、基本运算的考查.
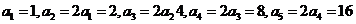 ,
,
易知 ,∴应填255.
,∴应填255.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com