8．设，是两条不同的直线，是一个平面，则下列命题正确的是

A．若，，则　　　 　　B．若，，则

C．若，，则　　　　 　　D．若，，则

7．已知点到直线的距离相等，则实数的值等于

A．-2或1　　　　　 B．1或2 　　　　　　C．-2或-1　　　　 D．-1或2

6．已知等差数列{}的前n项和为，若，则=

A． 68　　　　 B． 72 　　　　C．54　　　　 D． 90

5．“”是“函数在区间上为增函数”的

A．充分不必要条件 　B．必要不充分条件　　 C．充要条件　 D．既不充分也不必要条件

4．如右图是某几何体的三视图，其中正视图是腰长为2的等腰三角形，

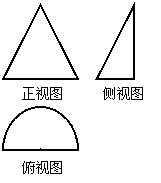俯视图是半径为1的半圆，则该几何体的体积是　

A．　　　 B．　 C．　　 D．

3．函数，，其中，则

．均为偶函数　　　　　 ．均为奇函数

． 为偶函数 ，为奇函数　　 ． 　为奇函数 ，为偶函数

2．函数的定义域是

．　．　　 ．　　 ．

1．全集, 集合，,则

．　　　　　　　　　　 ．

．　　　　 ．

9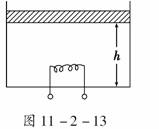．如图11－2－13所示，一圆柱形容器竖直放置，通过活塞封闭着

摄氏温度为t的理想气体．活塞的质量为m，横截面积为S，与容

器底部相距h.现通过电热丝给气体加热一段时间，结果活塞缓慢

上升了h，若这段时间内气体吸收的热量为Q，已知大气压强为

p₀，重力加速度为g，不计器壁向外散失的热量及活塞与器壁间的

摩擦，求：

(1)气体的压强；

(2)这段时间内气体的内能增加了多少？

(3)这段时间内气体的温度升高了多少？

解析：(1)p＝p₀+

(2)气体对外做功为

W＝pSh＝(p₀+)Sh＝(p₀S+mg)h

由热力学第一定律得：

ΔU＝Q－W＝Q－(p₀S+mg)h

(3)由盖­吕萨克定律得：＝

＝

解得：t′＝273+2t

Δt＝t′－t＝273+t.

答案：见解析

`

8．有人设计了一种测温装置，其结构如图11－2－12所示．玻璃泡A内封有一定量气体，与管A相连的B管插在水银槽中，管内水银面的高度x即可反映泡内气体的温度，即环境温度，并可由B管上的刻度直接读出．设B管的体积与A泡的体积相比可略去不计．

(1)B管刻度线是在1标准大气压下制作的(1标准大气压相当于76

cm水银柱的压强)．已知当温度t＝27℃时的刻度线在x＝16 cm处，

问t＝0℃的刻度线在x为多少厘米处？

(2)若大气压已变为相当于75 cm水银柱的压强，利用该测温装置测量温度时所得读数

仍为27℃，问此时实际温度为多少？

解析：(1)A中气体为等容过程，

有p＝p₁

把p₁＝76－16＝60 (cmHg)，

T₁＝273+27＝300 (K)，

T＝273 K代入上式得：

p＝×60 cmHg＝54.6 cmHg

x＝(76－54.6) cm＝21.4 cm

(2)此时A泡内气体压强为

p′＝p₀′－x＝75－16＝59 (cmHg)

而体积未变，由查理定律：

T′＝T₁＝×300 K＝295 K＝22℃.

答案：(1)21.4 cm　(2)22℃