
3.已知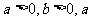 、
、 的等差中项是
的等差中项是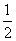 ,且
,且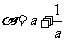 ,
,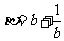 ,则
,则 的最小值是( )
的最小值是( )
A.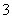 B. C.
B. C.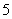 D.
D.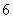
2.下列函数中,最小正周期为,且图像关于直线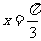 对称的是 ( )
对称的是 ( )
A. B.
B.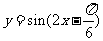 C.
C. D.
D.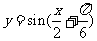
1.设集合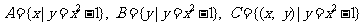 ,则下列关系中不正确的是( )
,则下列关系中不正确的是( )
A. B.
B.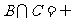 C.
C.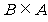 D.
D.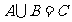
39.(2009上海卷文) 已知ΔABC的角A、B、C所对的边分别是a、b、c,设向量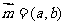 ,
,
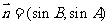 ,
, .
.
(1) 若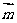 //
//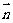 ,求证:ΔABC为等腰三角形;
,求证:ΔABC为等腰三角形;
(2) 若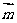 ⊥
⊥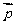 ,边长c = 2,角C =
,边长c = 2,角C = 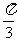 ,求ΔABC的面积 .
,求ΔABC的面积 .
证明:(1)
即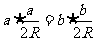 ,其中R是三角形ABC外接圆半径,
,其中R是三角形ABC外接圆半径,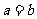

 为等腰三角形
为等腰三角形
解(2)由题意可知
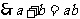
由余弦定理可知, 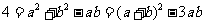






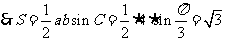
38.(2009湖南卷理)  在
在 ,已知
,已知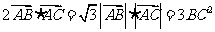 ,求角A,B,C的大小.
,求角A,B,C的大小.
解 设
由 得
得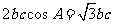 ,所以
,所以
又 因此
因此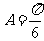


由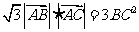 得
得 ,于是
,于是
所以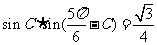 ,
,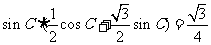 ,因此
,因此
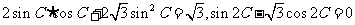 ,既
,既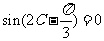
由A= 知
知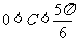 ,所以
,所以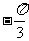 ,
,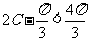 ,从而
,从而
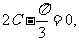 或
或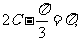 ,既
,既 或
或 故
故
 或
或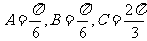 。
。
37.(2009湖南卷文)已知向量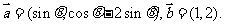
(1)若 ,求
,求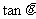 的值;
的值; 

(2)若 求
求 的值。
的值。
解 (1) 因为 ,所以
,所以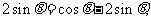
于是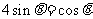 ,故
,故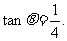
(2)由 知,
知,
所以
从而 ,即
,即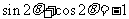 ,
,
于是 .又由
.又由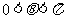 知,
知, ,
,
所以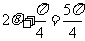 ,或
,或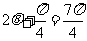 .
.
因此 ,或
,或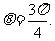
36.(2009广东卷理)已知向量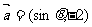 与
与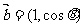 互相垂直,其中
互相垂直,其中 .
.
(1)求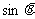 和
和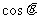 的值;
的值;
(2)若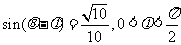 ,求
,求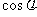 的值.
的值.
解 (1)∵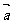 与
与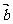 互相垂直,则
互相垂直,则 ,即
,即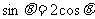 ,代入
,代入 得
得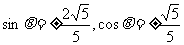 ,又
,又 ,
,
∴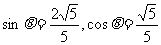 .
.
(2)∵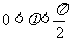 ,
,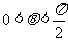 ,∴
,∴ ,
,
则 ,
,
35.(2009江苏卷)设向量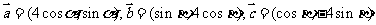
(1)若 与
与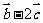 垂直,求
垂直,求 的值;
的值;

(2)求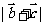 的最大值;
的最大值;
(3)若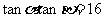 ,求证:
,求证: ∥
∥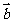 .
. 
解析 本小题主要考查向量的基本概念,同时考查同角三角函数的基本关系式、二倍角的正弦、两角和的正弦与余弦公式,考查运算和证明得基本能力。满分14分。

34.(2009年广东卷文)(已知向量 与
与 互相垂直,其中
互相垂直,其中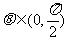
(1)求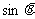 和
和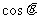 的值
的值
(2)若 ,
,
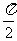 ,求
,求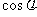 的值
的值
解 (1)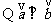 ,
,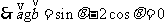 ,即
,即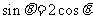
又∵ , ∴
, ∴ ,即
,即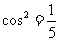 ,∴
,∴
又 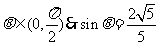 ,
,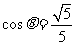
(2) ∵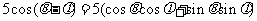

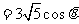
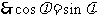 ,
,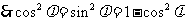 ,即
,即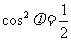
又 
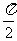 , ∴
, ∴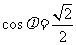


33.(2009辽宁卷文)在平面直角坐标系xoy中,四边形ABCD的边AB∥DC,AD∥BC,已知点
A(-2,0),B(6,8),C(8,6),则D点的坐标为___________.
答案 (0,-2)
解析 平行四边形ABCD中,
∴ =(-2,0)+(8,6)-(6,8)=(0,-2)
=(-2,0)+(8,6)-(6,8)=(0,-2)
即D点坐标为(0,-2)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com