3]普通高中数学课程标准实验教科书数学必修(1)(2)(4)(5) [M].人民教育出版社.

2]曹时武 数学概念课的教学模式探讨[J]. 中学数学 2007.­12

1]邱僖 关于概念课教学的研究[J]. 中学数学 2007.9

4、通过解决实际问题，深入理解数学概念的本质

很多数学概念都有其实际背景, 它的产生必然离不开现实世界,离不开生活实际, 反过来, 在概念形成后, 学会在实际问题中运用所学概念, 这也是深入理解概念本质的有效途径。如学习“等比数列”概念之后，可解决实际问题：“今有出门望见九堤，堤有九木，木有九枝，枝有九巢，巢有九禽，禽有九雏，雏有九毛，毛有九色，问各有几何？。利用统计中的“方差”概念, 通过对几组数据的分析, 判断某事件(如射击、成绩、机器性能等)的稳定性等等, 通过解决这些实际问题,能够极大提高学生运用概念的灵活性,并对概念的本质有更深入的理解。

总之，在概念教学中，要根据课标对概念教学的具体要求，创造性地使用教材。优化概念教学设计，把握概念教学过程，真正使学生在参与的过程中产生内心的体验和创造。

参考文献：

3、将所学概念纳入到相应的概念体系，形成一个整体

因为任何数学概念都不是孤立存在的，前后概念之间彼此联系密切，所以掌握概念必须在概念体系中把握。如在“抛物线的定义”教学中，教师引导学生将椭圆、双曲线与抛物线概念的本质属性进行比较，把焦点和相应准线相同的三种曲线在同一个图形中作出，使学生了解到三种曲线之间的逻辑关系，并把抛物线概念与椭圆、双曲线一起纳入到了圆锥曲线的概念体系中，形成一个整体。通过建立概念链或概念网络, 使学生深入理解数学概念的本质，从而使所学概念类化。

2、通过开放性问题与变式, 深入理解数学概念

数学概念形成之后，通过开放性问题,引导学生从不同角度理解概念。这将影响学生对数学概念的巩固，以及解题能力的形成。如在“等比数列”中设置问题：

例：已知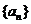是等比数列且公比为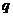，请你构造出新的等比数列，并指出它们的公比。

变式：已知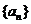,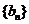是项数相同的等比数列，公比分别为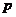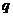，，请你构造出新的等比数列，并指出它们的公比。

通过学生的讨论与辨析，让学生对等比数列的概念有了一个更深入的理解与认识。

数学概念的深刻理解并牢固掌握, 其目的是为了能够灵活、正确地运用它, 同时, 在运用的过程中,又能更进一步地深化对数学概念的本质的理解。为此,在教学中应采用多种形式, 引导学生在运算、推理、证明及解决问题的过程中运用数学概念。

1、通过反例辩析，及时巩固概念

在中学数学教学中， 很多数学概念(如函数、函数的单调性、奇偶性的定义等)都采用正面阐述的形式，而这些重要概念是解题的基础，若学生对其本质属性含糊不清， 就会在解题过程中混淆、偷换概念， 造成解题失误。为了准确把握概念的本质，可以利用反例来加深对概念的理解。如：

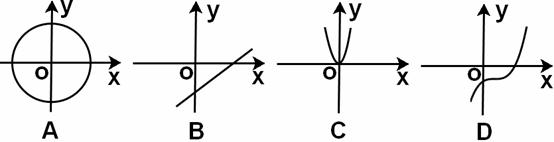例：下列图形中，不可能是函数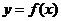的图象是(　　 )

通过观察、比较，同学们认识到：对于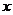在某个范围内的每一个确定的值，按照某种对应法则，变量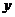都是唯一确定的值和它对应，这才是构成函数关系的本质。所以只能选A。

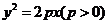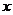又如在教学“导数”这一章时，教材中是用割线的极限位置来定义切线的，为此，可以提出以下问题：为什么不说“与曲线只有一个公共点的直线叫做切线”? 直线与曲线相切, 是否一定只有一个公共点? 对于这两个问题都要通过构造反例进行研究，前一个问题的反例是:抛物线与轴、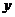轴都只有一个公共点, 但只有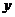轴是它的切线, 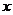轴显然不是它的切线；或者与双曲线的渐近线平行的直线与双曲线也只有一个公共点。但它也不是其切线，因此与曲线只有一个公共点的直线不一定是切线，它只符合圆、椭圆等一类曲线。后一个问题也可以举出下列反例，已知曲线C: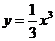。可求出曲线C上横坐标为2的点处的切线方程是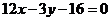，但它与曲线C的公共点除了切点外,还有另外一个公共点是(-4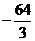，)。通过此例可以说明:直线与曲线相切不一定只有一个公共点。当曲线是二次曲线时, 能够保证直线与曲线相切有且只有一个公共点。所以，若能举出恰当的反例加以说明, 会起到正面强调所无法发挥的强化作用, 使概念理解得更加深刻。

3、运用比较, 区分异同。许多数学概念, 由于表示它们的符号、词语和概念本身的含义相似, 可能产生概念间的互相干扰、互相混淆, 教学中应引导学生进行归类比较, 分析两种概念的从属关系, 区分它们的异同之处。如: 充分条件与必要条件; 排列与组合; 三棱锥与四面体; 否命题与命题的否定; 等等, 从而促进学生对概念的本质有更深刻的认识。

2、抓住要点, 促进概念的深化。揭示概念的内涵不仅由概念的定义完成, 还常常由定义所推出的一些定理、公式得到进一步揭示。如三角函数定义教学中, 同角三角函数关系式、诱导公式、三角函数值的符号规律、两角和与差的三角函数、 三角函数的图象和性质都是由定义推导出来的, 可使学生清楚地看到概念是学习其它知识的依据, 反过来又会使三角函数定义的内涵得到深刻揭示, 加深对概念的理解, 增强运用概念进行推理判断的思维能力。教学中应有意识地启发学生提高认识, 引导学生从概念出发, 逐步深入展开对它所反映的数学模式作深入的探究, 以求更深刻地认识客观规律。

数学概念是多结构、多层次的。理解和掌握数学概念, 应遵循由具体到抽象, 由低级到高级, 由简单到复杂的认知规律。因此, 一个数学概念的建立和形成, 应该通过学生的亲身体验、主动构建, 通过分析、比较、归纳等方式, 揭示出概念的本质属性, 形成完整的概念链, 从而加强学生分析问题, 解决问题的能力, 形成学生的数学思想。可以从以下几方面给予指导。

1、分析构成概念的基本要素。数学概念的定义是用精练的数学语言概括表达出来的, 在教学中, 抽象概括出概念后, 还要注意分析概念的定义, 帮助学生认识概念的含义。如为了使学生能更好地掌握函数概念, 我们必须揭示其本质特征, 进行逐层剖析。对定义的内涵要阐明三点：①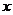、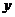的对应变化关系。例如在“函数的表示方法”一节例4的教学，教师要讲明并强调每位同学的“成绩”与“测试时间”之间形成函数关系，使学生明白并非所有的函数都有解析式，由此加深学生对函数的“对应法则”的认识。②实质：每一个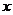值，对应唯一的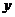值，可例举函数讲解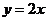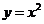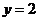：，，都是函数，但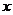、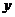的对应关系不同，分别是一对一、二对一、多对一，从而加深对函数本质的认识。再通过图象显示，使学生明白，并非随便一个图形都是函数的图象，从而掌握能成为一个函数图象的图形的条件特征。③定义域，值域，对应法则构成函数的三素，缺一不可，但要特别强调定义域的重要性。由于学生学习解析式较早，比较熟悉，他们往往只关注解析式，忽略定义域而造成错误。为此可让学生比较我函数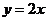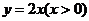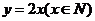，，的不同并分别求值域，然后结合图象分析得出：三者大相径庭！强调解析式相同但定义域不同的函数决不是相同的函数。再结合分段函数和有实际意义的函数，以引导他们对实际问题的关注和思考。