
7、动态几何与几何演变 8、实际应用问题
3、代数与几何综合题 4、开放探究性问题
1、代数综合题 2、几何综合题
2、在平面直角坐标系中,ΔAOB的位置如图所示,已知∠AOB=90°,AO=BO,点A的坐标为(-3,1).
(1)求点B的坐标;
(2)求过A、O、B三点的抛物线的解析式;
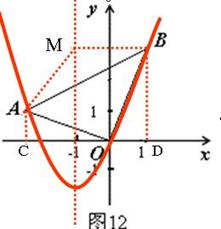 (3) 抛物线的对称轴上有一点M,且点M的纵坐标与点B的纵坐标相等,连结AM、BM.求ΔAMB的面积.
(3) 抛物线的对称轴上有一点M,且点M的纵坐标与点B的纵坐标相等,连结AM、BM.求ΔAMB的面积.
解:(1)过点A作AC⊥x轴于点C,
过点B作BD⊥x轴于点D,
∵ ∠AOB=90°,
∴ ∠AOC=∠OBD
∵ ∠ACO=∠ODB=90°, AO=BO
∴ΔACO≌ΔODB
∴OD=CA=1,BD=CO=3
∴点B的坐标为(1,3).
(2)设函数解析式为y=ax2+bx(a≠0)
 可得 9a-3b=1
可得 9a-3b=1
a+b=3
解得: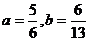
 此解析式为
此解析式为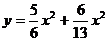
(3)解得对称轴 x=-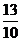
∴
M点坐标为( -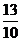 ,3)
,3)
则BM=|1 –(-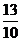 )| =
)| =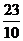
MB边上的高=|3-1|=2
ΔABM的面积=2×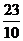 ÷ 2=
÷ 2=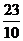
1、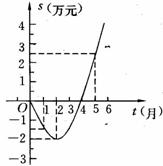 某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到盈利的过程.下面的二次函数图像(部分)刻画了该公司年初以来累积利润s(万元)与销售时间t(月)之间的关系(即前t个月的利润总和s与t之间的关系).根据图像提供的信息,解答下列问题:
某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到盈利的过程.下面的二次函数图像(部分)刻画了该公司年初以来累积利润s(万元)与销售时间t(月)之间的关系(即前t个月的利润总和s与t之间的关系).根据图像提供的信息,解答下列问题:
(1)由已知图像上的三点坐标,求累积利润s(万元)与时间t(月)之间的函数关系式;
(2)求截止到几月末公司累积利润可达到30万元.
解:(1) 设s与t之间的函数关系式为s=at2+bt+c(a ≠0)
由题意可得 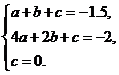 解得
解得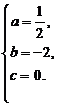
∴s=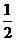 t2-2t.
t2-2t.
(2)把s=30代入s=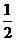 t2-2t, 得30=
t2-2t, 得30=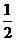 t2-2t.
t2-2t.
解得t1=10,t2=-6(舍).
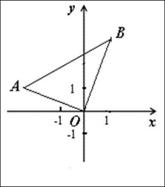 答:截止到10月末公司累积利润可达到30万元.
答:截止到10月末公司累积利润可达到30万元.
解此类型的题,要数型结合;用待定系数法,求出函数关系式;再利用函数的性质解决一些实际问题.注意完善解题的步骤,把握好此类型的题的得分点.
例1(2008兰州)一座拱桥的轮廓是抛物线型(如图1所示),拱高6m,跨度20m,相邻两支柱间的距离均为5m.
(1)将抛物线放在所给的直角坐标系中(如图2所示),求抛物线的解析式;
(2)求支柱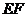 的长度;
的长度;
(3)拱桥下地平面是双向行车道(正中间是一条宽2m的隔离带),其中的一条行车道能否并排行驶宽2m、高3m的三辆汽车(汽车间的间隔忽略不计)?请说明你的理由.(共10分)
解:(1)根据题目条件, 的坐标分别是
的坐标分别是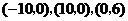 .······························ 1分
.······························ 1分
设抛物线的解析式为y=ax2+bx+c,············································································· 2分
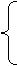 将
将 的坐标代入y=ax2+bx+c,得 100a-10b+c=0
的坐标代入y=ax2+bx+c,得 100a-10b+c=0
100a+10b+c=0
c=6··············· 3分
解得a=-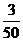 ,b=0,c=6.··············································· 4分
,b=0,c=6.··············································· 4分
所以抛物线的表达式是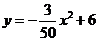 .····················· 5分
.····················· 5分
(2)可设 ,于是
,于是
 ························································································· 6分
························································································· 6分
从而支柱EF的长度是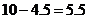 米.··································································· 7分
米.··································································· 7分

(3)设 是隔离带的宽,
是隔离带的宽,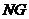 是三辆车的宽度和,
是三辆车的宽度和,
则 点坐标是
点坐标是 .······························································································· 8分
.······························································································· 8分
过 点作
点作 垂直
垂直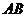 交抛物线于
交抛物线于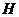 ,则
,则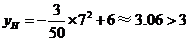 .················ 9分
.················ 9分
根据抛物线的特点,可知一条行车道能并排行驶这样的三辆汽车.····························· 10分
例2、(2008内江)如图4,小明的父亲在相距2米的两棵树间拴了一根绳子,给他做了一个简易的秋千,拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子,则绳子的最低点距地面的距离为 米.
|
|

 分析:如果把左边的树子看成纵轴,地平线看成横轴,则
分析:如果把左边的树子看成纵轴,地平线看成横轴,则
A (0, 2.5), B (2, 2.5), C (0.5, 1)
|
 解析式可得一个方程组 c=2.5
解析式可得一个方程组 c=2.5
4a+2b+c=2.5
0.25a+0.5b+c=1
解之得:a=2, b=-4, c=2.5
所以y= 2x2-4x+2.5
当x=1时, y=2-4+2.5=0.5
10. D。“wugging”、“students”和“charity”是该文话题中的三个重要元素,因此D项标题最具针对性
9. C。从倒数第二段可知,学生和慈善团体均受益于,因此C项正确。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com