
科目: 来源: 题型:
【题目】综合与实践
问题情境
数学活动课上,老师让同学们根据如下问题情境,发现并提出问题.
如图1,△ABC与△EDC都是等腰直角三角形,点E,D分别在AC和BC上,连接EB.将线段EB绕点B顺时针旋转90°,得到的对应线段为BF.连接DF.“兴趣小组”提出了如下两个问题:①AE=BD,AE⊥BD;②DF=AB,DF⊥AB.
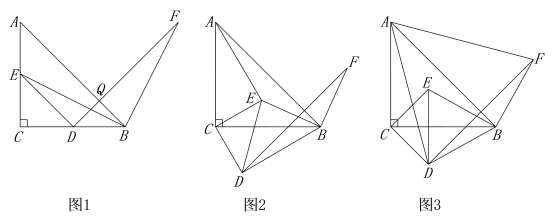
解决问题:
(1)请你证明“兴趣小组”提出的第②个问题.
探索发现:
(2)“实践小组”在图1的基础上,将△EDC绕点C顺时针旋转角度![]() (0°<
(0°<![]() <90°),其它条件保持不变,得到图2.
<90°),其它条件保持不变,得到图2.
①请你帮助“实践小组”探索:“兴趣小组”提出的两个问题是否还成立?如果成立,请给出证明;若不成立,请说明理由.
②如图3,当AD=AF时,请求出此时旋转角α的大小.
查看答案和解析>>
科目: 来源: 题型:
【题目】晋阳湖公园是华北最大的城市公园,是太原市未来的“城市客厅”,是工业文明与人文历史的交融.园内的晋阳湖是华北最大的人工湖,素称“中国北湖”.为满足晋阳湖景区水秀综合演艺的调试和表演用水需求,工程部按计划从4月1日开始向晋阳湖公园南扩湖供水,供水总量为120万立方米,经过计算,如果将原计划的每日供水量提高25%,则完成供水所需的时间将比原计划时间提前6天完成.
(1)求原计划每日的供水量与供水的天数分别是多少?
(2)工程部按原计划供水12天后,接到上级指挥部的命令,要求工程部务必与4月28日前完成供水任务.则在后一阶段的供水中,至少需将每日的供水量提高百分之多少,才能在指挥部要求的期限内完成供水任务?
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下列材料,解决所提的问题:
勾股定理a+b=c本身就是一个关于a,b,c的方程,我们知道这个方程有无数组解,满足该方程的正整数解(a,b,c)通常叫做勾股数组.关于勾股数组的研究我国历史上有非常辉煌的成就,根据我国古代数学书《周髀算经》记载,在约公元前1100年,人们就已经知道“勾广三、股修四、径隅五”(古人把较短的直角边称为勾,较长的直角边称为股,而斜边则为弦),即知道了勾股数组(3,4,5).类似地,还可以得到下列勾股数组:(3,4,5),(5,12,13),(7,24,25),(9,40,41),…等等,这些数组也叫做毕达哥拉斯勾股数组.
上述勾股数组的规律,可以用下面表格直观表示:
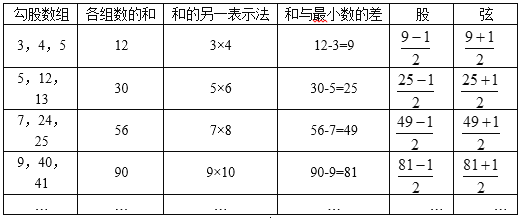
观察分析上述勾股数组,可以看出它们具有如下特点:
特点1:最小的勾股数的平方等于另两个勾股数的和;
特点2:____________________________________.
…
学习任务:
(1)请你再写出上述勾股数组的一个特点:________________;
(2)如果n表示比1大的奇数,则上述勾股数组可以表示为(n,______,______)
(3)请你证明(2)的结论.
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司招聘一名职员,先对应聘者进行笔试考核,笔试进入前两名的选手再进入面试方面的考核,最终在参加面试的两人中录取一人.该公司将应聘者的笔试成绩划分了4个等级:设应聘者的成绩为x(单位:分),当60≤x<70时为不合格;当70≤x<80时为合格;当80≤x<90时为良好;当90≤x≤100时为优秀.下面是参加笔试的10名应聘者的成绩:86 75 67 86 92 75 82 90 86 78
(1)这10名应聘者的笔试成绩的中位数是_______,众数是_______;
(2)请将下面表示上述4个等级的统计图补充完整;
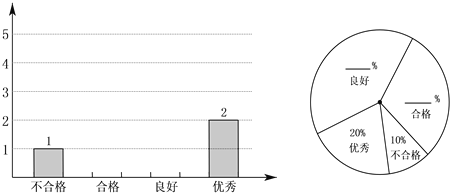
(3)该公司对进入笔试前两名的甲、乙二人进行了面试考核,面试中包括形体、口才、人际交往、创新能力,他们的成绩(百分制)如下表:
候选人 | 面试项目 | |||
形体 | 口才 | 人际交往 | 创新能力 | |
甲 | 86 | 90 | 95 | 90 |
乙 | 95 | 85 | 90 | 92 |
如果公司根据经营性质和岗位要求,以面试成绩中形体占10%,口才占20%,人际交往40%,创新能力占30%确定成绩,那么你认为该公司应该录取谁?请通过计算说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在矩形ABCD中,O为AC的中点,直线EF经过点O,并且与AB交于点E,与DC交于点F,∠DFE=∠BFE.
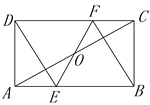
(1)求证:四边形DEBF是菱形;
(2)若AD=4,AB=8,则线段EF的长是_______.(直接写出答案即可)
查看答案和解析>>
科目: 来源: 题型:
【题目】在太原迎泽西大街上有一种智能垃圾桶,这种智能垃圾桶不仅可以供行人休息,灯箱边的中部还有USB接口可供行人充电.此种垃圾桶的侧面示意图如图所示,其中AC∥ED,AB∥EF∥GH,CD=20cm,DE=60cm,EF=100m,GH=80cm,∠CDE=∠EFG=90°,∠DEF=130°,则此种垃圾桶的高度(C到地面的距离)约为________cm.(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)
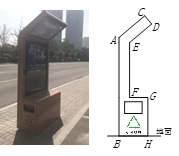
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示是一个圆形飞镖靶的示意图,其中A,B,C,D,E,F是⊙O的六等分点,如果向该飞镖靶上任意投一枚飞镖,则飞镖落在阴影区域的概率是_______.
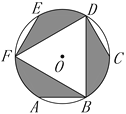
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在过直线AB外一点P作直线AB的平行线时,可以按如下步骤进行:①在直线AB上任取两点C,D;②分别以点P,D为圆心,CD与PC为半径画弧,两弧交于点E;③作直线PE,则PE∥AB.在上面作图过程中,PE∥AB的依据是________.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AB是⊙O的直径,点C为⊙O上一点,过点C作⊙O的切线,交直径AB的延长于点D,若∠ABC=65°,则∠D的度数是( )

A.25°B.30°C.40°D.50°
查看答案和解析>>
科目: 来源: 题型:
【题目】对于直角坐标系 xOy 中的点P和⊙C,给出如下定义:若⊙C上存在两个点A,B,使得点P在射线BC上,且∠APB=![]() ∠ACB(0°<∠ACB<180°),则称P为⊙C的依附点.
∠ACB(0°<∠ACB<180°),则称P为⊙C的依附点.
(1)当⊙O的半径为1时
①已知点D(﹣1,0),E(0,﹣2),F(2.5,0),在点D,E,F中,⊙O的依附点是___;
②点T在直线y=![]() x上,若T为⊙O的依附点,求点T的横坐标t的取值范围;
x上,若T为⊙O的依附点,求点T的横坐标t的取值范围;
(2)⊙C的圆心在x轴上,半径为1,直线 y=﹣2x+2与x轴、y 轴分别交于点M、N,若线段MN上的所有点都是⊙C 的依附点,请求出圆心C的横坐标n的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com