
科目: 来源: 题型:
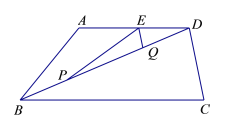
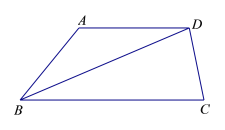
【题目】如图,在梯形ABCD中,AD∥BC,BC=BD=10,CD=4,AD=6.点P是线段BD上的动点,点E、Q分别是线段DA、BD上的点,且DE=DQ=BP,联结EP、EQ.
(1)求证:EQ∥DC;
(2)如果△EPQ是以EQ为腰的等腰三角形,求线段BP的长;
(3)当BP=m(0<m<5)时,求∠PEQ的正切值.(用含m的式子表示)
查看答案和解析>>
科目: 来源: 题型:
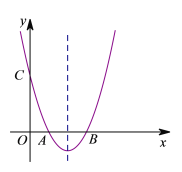
【题目】如图,在平面直角坐标系xOy中,抛物线![]() 与x轴交于A、B两点,与y轴交于点C,对称轴为直线x=2,点A的坐标为(1,0).
与x轴交于A、B两点,与y轴交于点C,对称轴为直线x=2,点A的坐标为(1,0).
(1)求该抛物线的表达式及顶点坐标;
(2)点P为抛物线上一点(不与点A重合),联结PC.当∠PCB=∠ACB时,求点P的坐标;
(3)在(2)的条件下,将抛物线沿平行于![]() 轴的方向向下平移,平移后的抛物线的顶点为点D,点P关于x轴的对应点为点Q,当OD⊥DQ时,求抛物线平移的距离.
轴的方向向下平移,平移后的抛物线的顶点为点D,点P关于x轴的对应点为点Q,当OD⊥DQ时,求抛物线平移的距离.

查看答案和解析>>
科目: 来源: 题型:
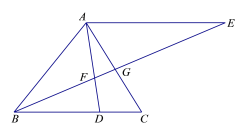
【题目】已知:如图,在△ABC中,点D在边BC上,AE∥BC,BE与AD、AC分别相交于点F、G, ![]() .
.
(1)求证:△CAD∽△CBG;
(2)联结DG,求证:![]() .
.
查看答案和解析>>
科目: 来源: 题型:
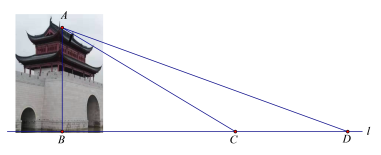
【题目】水城门位于淀浦河和漕港河三叉口,是环城水系公园淀浦河梦蝶岛区域重要的标志性景观.在课外实践活动中,某校九年级数学兴趣小组决定测量该水城门的高.他们的操作方法如下:如图,先在D处测得点A的仰角为20°,再往水城门的方向前进13米至C处,测得点A的仰角为31°(点D、C、B在一直线上),求该水城门AB的高.(精确到0.1米)
(参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
查看答案和解析>>
科目: 来源: 题型:
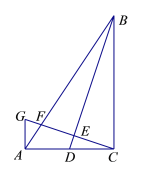
【题目】如图,在Rt△ABC中,∠ACB=90,AC=2,BC=3.点D为AC的中点,联结BD,过点C作CG⊥BD,交AC的垂线AG于点G,GC分别交BA、BD于点F、E.
(1)求GA的长;
(2)求△AFC的面积.
查看答案和解析>>
科目: 来源: 题型:
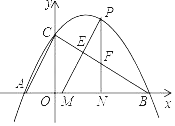
【题目】如图,二次函数y=ax2+bx+![]() 的图象经过A(﹣1,0),B(3,0),与y轴相交于点C.点P为第一象限的抛物线上的一个动点,过点P分别做BC和x轴的垂线,交BC于点E和F,交x轴于点M和N.
的图象经过A(﹣1,0),B(3,0),与y轴相交于点C.点P为第一象限的抛物线上的一个动点,过点P分别做BC和x轴的垂线,交BC于点E和F,交x轴于点M和N.
(1)求这个二次函数的解析式;
(2)求线段PE最大值,并求出线段PE最大时点P的坐标;
(3)若S△PMN=3S△PEF时,求出点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读材料:各类方程的解法
求解一元一次方程,根据等式的基本性质,把方程转化为x=a的形式.求解二元一次方程组,把它转化为一元一次方程来解;类似的,求解三元一次方程组,把它转化为解二元一次方程组.求解一元二次方程,把它转化为两个一元一次方程来解.求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生增根,所以解分式方程必须检验.各类方程的解法不尽相同,但是它们有一个共同的基本数学思想![]() 转化,把未知转化为已知.
转化,把未知转化为已知.
用“转化”的数学思想,我们还可以解一些新的方程.例如,一元三次方程x3+x2-2x=0,可以通过因式分解把它转化为x(x2+x-2)=0,解方程x=0和x2+x-2=0,可得方程x3+x2-2x=0的解.
(1)问题:方程x3+x2-2x=0的解是x1=0,x2= ,x3= ;
(2)拓展:用“转化”思想求方程![]() 的解;
的解;
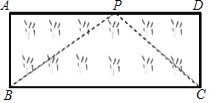
(3)应用:如图,已知矩形草坪ABCD的长AD=8m,宽AB=3m,小华把一根长为10m的绳子的一端固定在点B,沿草坪边沿BA,AD走到点P处,把长绳PB段拉直并固定在点P,然后沿草坪边沿PD、DC走到点C处,把长绳剩下的一段拉直,长绳的另一端恰好落在点C.求AP的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,等腰直角△ABC中,CA=CB,点E为△ABC外一点,CE=CA,且CD平分∠ACB交AE于D,且∠CDE=60°.
(1)求证:△CBE为等边三角形;
(2)若AD=5,DE=7,求CD的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】某学校准备采购一批茶艺耗材和陶艺耗材.经查询,如果按照标价购买两种耗材,当购买茶艺耗材的数量是陶艺耗材数量的2倍时,购买茶艺耗材共需要18000元,购买陶艺耗材共需要12000元,且一套陶艺耗材单价比一套茶艺耗材单价贵150元.
(1)求一套茶艺耗材、一套陶艺耗材的标价分别是多少元?
(2)学校计划购买相同数量的茶艺耗材和陶艺耗材.商家告知,因为周年庆,茶艺耗材的单价在标价的基础上降价2![]() 元,陶艺素材的单价在标价的基础降价150元,该校决定增加采购数量,实际购买茶艺素材和陶艺素材的数量在原计划基础上分别增加了2.5
元,陶艺素材的单价在标价的基础降价150元,该校决定增加采购数量,实际购买茶艺素材和陶艺素材的数量在原计划基础上分别增加了2.5![]() %和
%和![]() ,结果在结算时发现,两种耗材的总价相等,求
,结果在结算时发现,两种耗材的总价相等,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线y=﹣x+1与x轴,y轴分别交于B,A两点,动点P在线段AB上移动,以P为顶点作∠OPQ=45°交x轴于点Q.

(1)求点A和点B的坐标;
(2)比较∠AOP与∠BPQ的大小,说明理由.
(3)是否存在点P,使得△OPQ是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com