
科目: 来源: 题型:
【题目】某年级共有150名女生,为了解该年级女生实心球成绩(单位:米)和一分钟仰卧起坐成绩(单位:个)的情况,从中随机抽取30名女生进行测试,获得了他们的相关成绩,并对数据进行整理、描述和分析.下面给出了部分信息.
a. 实心球成绩的频数分布表如下:
分组 |
|
|
|
|
|
|
频数 | 2 | m | 10 | 6 | 2 | 1 |
b. 实心球成绩在![]() 这一组的是:
这一组的是:
a7.0 7.0 7.0 7.1 7.1 7.1 7.2 7.2 7.3 7.3
c. 一分钟仰卧起坐成绩如下图所示:
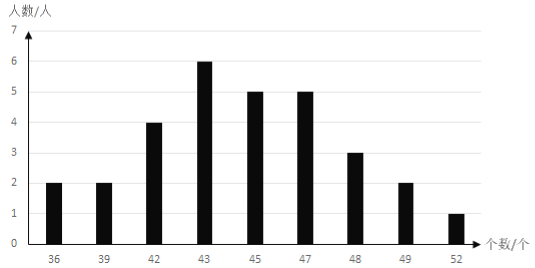
根据以上信息,回答下列问题:
(1) ①表中m的值为__________;
②一分钟仰卧起坐成绩的中位数为__________;
(2)若实心球成绩达到7.2米及以上时,成绩记为优秀.
①请估计全年级女生实心球成绩达到优秀的人数;
②该年级某班体育委员将本班在这次抽样测试中被抽取的8名女生的两项成绩的数据抄录如下:
女生代码 | A | B | C | D | E | F | G | H |
实心球 | 8.1 | 7.7 | 7.5 | 7.5 | 7.3 | 7.2 | 7.0 | 6.5 |
一分钟仰卧起坐 | * | 42 | 47 | * | 47 | 52 | * | 49 |
其中有3名女生的一分钟仰卧起坐成绩未抄录完整,但老师说这8名女生中恰好有4人两项测试成绩都达到了优秀,于是体育委员推测女生E的一分钟仰卧起坐成绩达到了优秀,你同意体育委员的说法吗?并说明你的理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AB为⊙O的直径,且AB=4,点C是弧AB上的一动点(不与A,B重合),过点B作⊙O的切线交AC的延长线于点D,点E是BD的中点,连接EC.
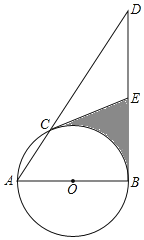
(1)若BD=8,求线段AC的长度;
(2)求证:EC是⊙O的切线;
(3)当∠D=30°时,求图中阴影部分面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在边长为1的菱形ABCD中,∠ABC=120°,P是边AB上的动点,过点P作PQ⊥AB交射线AD于点Q,连接CP,CQ,则△CPQ面积的最大值是( )
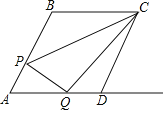
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,小明站在某广场一看台C处,从眼睛D处测得广场中心F的俯角为21°,若CD=1.6米,BC=1.5米,BC平行于地面FA,台阶AB的坡度为i=3:4,坡长AB=10米,则看台底端A点距离广场中心F点的距离约为(参考数据:sin21°≈0.36,cos21°≈0.93,tan21°≈0.38)( )
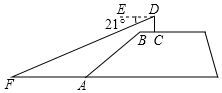
A.8.8米B.9.5米C.10.5米D.12米
查看答案和解析>>
科目: 来源: 题型:
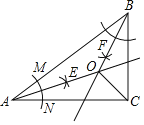
【题目】如图,在△ABC中,AB=10,AC=8,BC=6.按以下步骤作图:
①以A为圆心,任意长为半径作弧,分别交AB,AC于点M,N;
②分别以M,N为圆心,以大于![]() MN的长为半径作弧,两弧交于点E;
MN的长为半径作弧,两弧交于点E;
③作射线AE;
④以同样的方法作射线BF,AE交BF于点O,连结OC,则OC为( )
A.2![]() B.2C.
B.2C.![]() D.1
D.1
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下面材料,并回答问题:
定义:平面内与一个定点F和一条定直线l(l不经过点F)距离相等的所有点组成的图形叫抛物线.点F叫做抛物线的焦点,直线l叫做抛物线的准线.
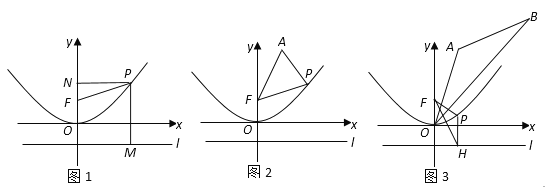
应用:(1)如图1,一条抛物线的焦点为F(0,1),准线为过点(0,-1)且平行于x轴的直线l;设点P(x,y)为抛物线上任意一点,小聪同学在应用定义求这条抛物线的解析式时作出了如下不完整的解答,请你将余下部分补充出来.
解:设点P(x,y)为抛物线上任意一点,作PM⊥l于点M,则PM=_________
作PN⊥y轴于点N,则在△PFN中,有PN=![]() ,NF=
,NF=![]() ,所以PF=__________
,所以PF=__________
∵PF=PM
∴_________=____________,
将方程两边同时平方,解得抛物线的解析式为_____________
(2)如图2,在(1)的条件下,点A(1,3)是坐标平面内一点,则△FAP的周长最小值为________
(3)在(1)(2)的条件下,如图3,点B(4,4)是坐标平面内另一点,过P作PH⊥l,垂足为H,连接PF和FH,问在抛物线上是否存在点P,使得以P,F,H为顶点的三角形与△ABO相似?若存在,求出P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在等腰Rt△ABC中,∠ABC=90°,AE平分∠BAC交BC于E,CD⊥AE交AE延长线于D,连接BD,若BD=CD,⊙O是以AE为直径的△ABE的外接圆,与AC交于点H.

(1)求证:BD为⊙O的切线;
(2)设⊙O的半径为1,BF平分∠ABC交AE于G,交⊙O于F;
①求![]() 的值.
的值.
②求BE2的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,矩形ABCD的对角线相交于O,E是OD的中点,DF∥AC交CE延长线于点F,连接AF.
(1)求证:四边形AODF是菱形.
(2)若∠AFC=90°,AB=2,求AD的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】某商店购进甲乙两种商品,甲的进货单价比乙的进货单价高20元,已知20个甲商品的进货总价与25个乙商品的进货总价相同.
(1)求甲、乙每个商品的进货单价;
(2)若甲、乙两种商品共进货100件,要求两种商品的进货总价不高于9000元,同时甲商品按进价提高10%后的价格销售,乙商品按进价提高25%后的价格销售,两种商品全部售完后的销售总额不低于10480元,问有哪几种进货方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com