
科目:gzsx 来源:2011年山东省兖州市高一上学期期末考试数学试卷 题型:解答题
(12分)如图,四棱锥P-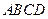 中,底面
中,底面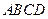 是正方形,
是正方形, 是正方形
是正方形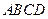 的中心,
的中心,
 底面
底面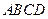 ,
, 是
是 的中点.
的中点.
求证:(1) ∥平面
∥平面 ;
;
(2)平面
 平面
平面 .
.
科目:gzsx 来源: 题型:044
如图,三棱锥P-ABC的底面ABC为等腰三角形,AB =AC =a ,侧棱长均为2a,问BC为何值时,三棱锥P-ABC的体积V最大,最大值是多少?

科目:gzsx 来源:数学教研室 题型:044

科目:gzsx 来源:数学教研室 题型:044

科目:gzsx 来源: 题型:044
如图,三棱锥P-ABC的底面ABC为等腰三角形,AB = AC = a
,侧棱长均为2a,问BC为何值时,三棱锥P-ABC的体积V最大,最大值是多少?
科目:gzsx 来源: 题型:
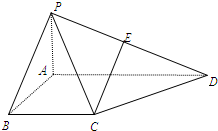 如图,四棱锥P-ABCD中,PA⊥平面ABCD,∠PBA=45°,底面ABCD为直角梯形,∠ABC=∠BAD=90°,PA=BC=
如图,四棱锥P-ABCD中,PA⊥平面ABCD,∠PBA=45°,底面ABCD为直角梯形,∠ABC=∠BAD=90°,PA=BC=| 1 | 2 |
科目:gzsx 来源: 题型:
 如图,四棱锥P-ABCD中,PA⊥平面ABCD,PB与底面所成的角为45°,底面ABCD为直角梯形,∠ABC=∠BAD=90°,E是PD的中点,且PA=BC=
如图,四棱锥P-ABCD中,PA⊥平面ABCD,PB与底面所成的角为45°,底面ABCD为直角梯形,∠ABC=∠BAD=90°,E是PD的中点,且PA=BC=| 1 | 2 |
科目:gzsx 来源: 题型:
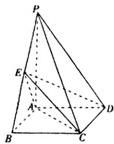 (2012•泰安二模)如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,PA=AB=
(2012•泰安二模)如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,PA=AB=| 2 |
科目:gzsx 来源: 题型:
 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,AB=2AD=2,BD=
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,AB=2AD=2,BD=| 3 |
| π |
| 6 |
科目:gzsx 来源: 题型:
 如图,四棱锥P-ABCD中,底面ABCD为菱形,∠DAB=60°,侧面PAD⊥平面AC,在△PAD中,E为AD中点,PA=PD.
如图,四棱锥P-ABCD中,底面ABCD为菱形,∠DAB=60°,侧面PAD⊥平面AC,在△PAD中,E为AD中点,PA=PD.| 2 |
科目:gzsx 来源: 题型:
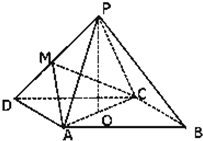 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠ADC=45°,AD=AC=2,O为AC的中点,PO⊥平面ABCD,PO=2,M为PD的中点,
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠ADC=45°,AD=AC=2,O为AC的中点,PO⊥平面ABCD,PO=2,M为PD的中点,科目:gzsx 来源: 题型:
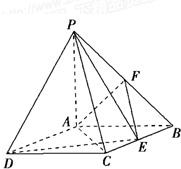 如图,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,AD=
如图,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,AD=| 3 |
科目:gzsx 来源: 题型:
 如图,四棱锥P-ABCD中,底面ABCD为等腰梯形,AB∥DC,AC⊥BD,O为AC,BD的交点,且PO⊥底面ABCD,OB=2,OD=1,OP=
如图,四棱锥P-ABCD中,底面ABCD为等腰梯形,AB∥DC,AC⊥BD,O为AC,BD的交点,且PO⊥底面ABCD,OB=2,OD=1,OP=| 2 |
| PM |
| MC |
科目:gzsx 来源: 题型:
 如图,四棱锥P-ABCD中,底面ABCD为矩形,PD垂直于底面ABCD,AD=PD=2,
如图,四棱锥P-ABCD中,底面ABCD为矩形,PD垂直于底面ABCD,AD=PD=2,| 2 |
科目:gzsx 来源: 题型:
 (2012•姜堰市模拟)如图,四棱锥P-ABCD中,底面ABCD是矩形,PD⊥平面ABCD,且PD=AD=1,AB=2,点E是AB上一点,且二面角P-EC-D的平面角为
(2012•姜堰市模拟)如图,四棱锥P-ABCD中,底面ABCD是矩形,PD⊥平面ABCD,且PD=AD=1,AB=2,点E是AB上一点,且二面角P-EC-D的平面角为| π | 4 |
科目:gzsx 来源: 题型:
 如图,四棱锥P-ABCD中,底面ABCD为菱形,PA⊥底面ABCD,AC=2
如图,四棱锥P-ABCD中,底面ABCD为菱形,PA⊥底面ABCD,AC=2| 2 |
科目:gzsx 来源: 题型:
 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,∠DAB=90°AD∥BC,AD⊥侧面PAB,△PAB是等边三角形,DA=AB=2,BC=
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,∠DAB=90°AD∥BC,AD⊥侧面PAB,△PAB是等边三角形,DA=AB=2,BC=| 1 | 2 |
科目:gzsx 来源: 题型:
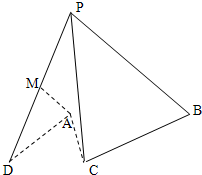 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB∥CD,AD=CD=1,∠BAD=120°,PA=
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB∥CD,AD=CD=1,∠BAD=120°,PA=| 3 |