
题目列表(包括答案和解析)
7、已知一个三角形的两边长是方程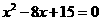 的根,则第三边y长的取值范围是………………………………………………………………………………………[ ]
的根,则第三边y长的取值范围是………………………………………………………………………………………[ ]
A、y<8 B、2<y<8 C、3<y<5 D、无法确定
6、一元二次方程-5x+3x2 =12 的二次项系数、一次项系数、常数项分别是……[ ]
A 、-5,3,12 B、 3,-5,12 C、3,-5,-12 D、-3,5,-12
5、下列方程①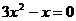 ;②
;②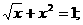 ③
③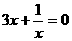 ;④
;④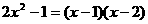 ;⑤
;⑤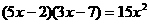 ,其中一元二次方程有…………………………………[ ]
,其中一元二次方程有…………………………………[ ]
A、1个 B、2个 C、3个 D、4个
4、把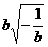 的根号外的因式移到根号内的结果是…………………………………[ ]
的根号外的因式移到根号内的结果是…………………………………[ ]
A、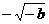 B、
B、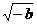 C、
C、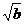 D、
D、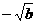
3、在式子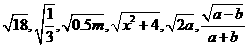 中,是最简二次根式的式子有[ ]个
中,是最简二次根式的式子有[ ]个
A、2 B、3 C、1 D、0
2、使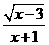 有意义的x的取值范围是……………………………………………[ ]
有意义的x的取值范围是……………………………………………[ ]
A、x ≥3 B、x ≥3且x≠-1 C、 x ≤3 D、x <3
1、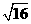 的平方根是………………………………………………………………[ ]
的平方根是………………………………………………………………[ ]
A、4 B、 -4 C、 ±4 D、±2
23. 我们把边长为1的等边三角形PQR沿着边长为整数的正n(n>3)边形的边按照如图(1)的方式连续转动,当顶点P回到正n边形的内部时,我们把这种状态称为它的“点回归”;当△PQR回到原来的位置时,我们把这种状态称它的“三角形回归”.
例如,如图(2)边长为1的等边三角形PQR的顶点P在边长为1的正方形ABCD内,顶点Q与点A重合,顶点R与点B重合,△PQR沿着正方形ABCD的边BC、CD、DA、AB、…、连续转动,当
△PQR连续转动3次时,顶点P回到正方形ABCD内部,第一次出现P的“点回归”; △PQR连续转动4次时△PQR回到原来的位置,出现第一次△PQR的“三角形回归”.
操作:
如图(3),如果我们把边长为1的等边三角形PQR沿着边长为1的正五边形ABCDE的边连续转动,则连续转动的次数k=________时,第一次出现P的“点回归”;连续转动的次数k=_________时,第一次出现△PQR的“三角形回归”.
猜想:我们把边长为1的等边三角形PQR沿着边长为1的正n(n>3)边形的边连续转动.
(1)连续转动的次数k=__________时,第一次出现P的“点回归”;
(2)连续转动的次数k=__________时,第一次出现△PQR的“三角形回归”;
(3)第一次同时出现P的 “点回归”与△PQR的“三角形回归”时,写出连续转动的次数k与正多边形的边数n之间的关系.
22.如图,在直线l上摆放有△ABC和直角梯形DEFG,且CD= 6㎝;在△ABC中:∠ACB=90°, ∠BAC=30°,AB=4㎝;在直角梯形DEFG中,EF∥DG, ∠DGF=90°, ∠EDG=60°,DG=6㎝,
DE=4㎝.
解答下列问题:
(1)旋转:将△ABC绕点C顺时针旋转90°得到对应的△A1B1C,求出AB1的长度.
(2)翻折:将△A1B1C沿过点B1且与l垂直的直线翻折,得到翻折后的对应图形△A2B1C1,试判定四边形A2B1DE的形状?并说明理由.
(3)平移:将△A2B1C1沿直线l向右平移至△A3B2C2,若设平移的距离为x (0≤x≤8),
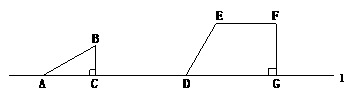 △A3B2C2与直角梯形重叠部分的面积为y,当y等于△ABC的面积的一半时,x的值是多少?
△A3B2C2与直角梯形重叠部分的面积为y,当y等于△ABC的面积的一半时,x的值是多少?
20.某水果批发商销售每箱进价为40元的苹果,物价部门规定每箱的利润不得高于40%,市场调查发现,若每箱以50元的价格销售,平均每天销售90箱;价格每提高一元,平均每天少销售3箱.
(1)若每箱销售价格提高2元,利润比提价前增加了还是减少了?增加或减少了多少?
(2)如果要使一天获得的利润为1125元,那么每箱售价应定为多少元?

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com