
22. (1)∵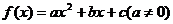 ,
,
∴ 由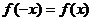 有
有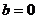 ,得
,得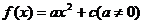 . ……………………2分
. ……………………2分
又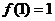 ,
,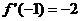 ,
,
∴ 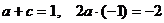 ,
,
解得 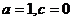 ,因此
,因此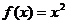 . ……………………5分
. ……………………5分
(2)∵ 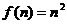
∴ 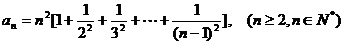 ,
,
于是 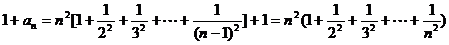 ,
,
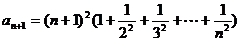 ,
,
因此 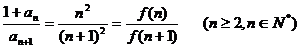 . ……………………9分
. ……………………9分
(3) 由题意可得 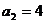 ;当
;当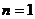 时,有
时,有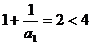 . ……………10分
. ……………10分
当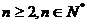 时,
时,
不等式左边=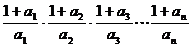
=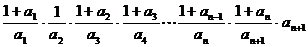 =
=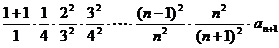 =
=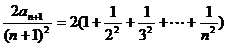 ……………………12分
……………………12分
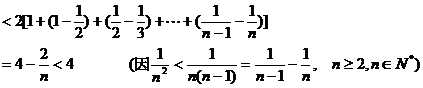
所以,对任意 有
有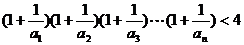 ……………………14分
……………………14分
21. (1)因为原点为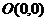 ,所以动点
,所以动点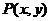 到原点的距离为
到原点的距离为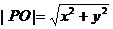 ,
,
∴ 动点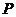 的坐标满足
的坐标满足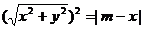 ,
,
∴ 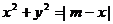 ,此即为动点
,此即为动点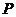 的轨迹方程. ……………………4分
的轨迹方程. ……………………4分
(2) 由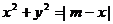 ,两边平方,移项因式分解,
,两边平方,移项因式分解,
得 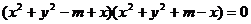 ,
,
∴ 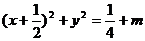 或
或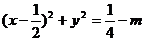 . ……………………6分
. ……………………6分

① 当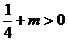 且
且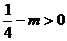 ,即
,即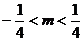 时,点
时,点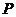 的轨迹是两个圆.一个圆的圆心是
的轨迹是两个圆.一个圆的圆心是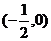 ,半径为
,半径为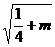 ;一个圆的圆心是
;一个圆的圆心是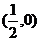 ,半径为
,半径为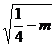 .……………………8分
.……………………8分
② 当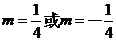 时,点
时,点 的轨迹是一个圆和一个点. ……………………10分
的轨迹是一个圆和一个点. ……………………10分
③ 当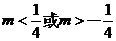 时,点
时,点 的轨迹是一个圆. ……………………12分
的轨迹是一个圆. ……………………12分
20. (1)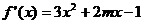 . ………………………………2分
. ………………………………2分
由题意 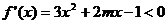 的解集是
的解集是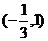 ,
,
即 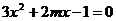 的两根分别是
的两根分别是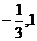 . ………………………………4分
. ………………………………4分
将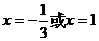 代入方程
代入方程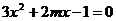 得
得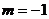 .
.
∴ 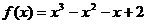 . ………………………………6分
. ………………………………6分
(2) 由题意知 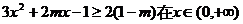 时恒成立,
时恒成立,
即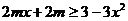 ,所以
,所以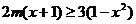 .
.
由于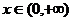 ,于是
,于是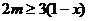 ,得
,得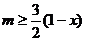 ……………9分
……………9分
而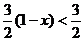 ,所以
,所以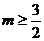 为所求. ………………………………12分
为所求. ………………………………12分
19. (1)张宁以2:1获胜即前两局战成1:1,第三局张宁胜.
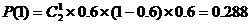 . ………………………………6分
. ………………………………6分
(2) 张宁失利包括0:2和1:2两种情况:
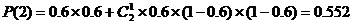 …………12分
…………12分
18. (1)∵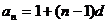 ,
,
∴ 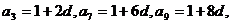 ………………………………3分
………………………………3分
于是 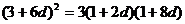 ,
,
注意到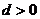 ,得
,得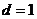 ,所以
,所以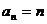 . ………………………………6分
. ………………………………6分
(2) 因为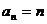 ,所以
,所以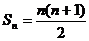 ,于是
,于是
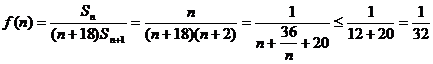
当且仅当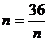 ,即
,即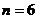 时,
时,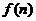 的最大值为
的最大值为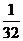 . ………………12分
. ………………12分
17. (1)由已知,可得 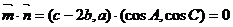 ,
,
即 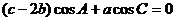 . ………………………………2分
. ………………………………2分
由正弦定理,得 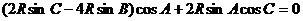 ,
,
∴ 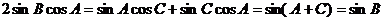 ,
,
由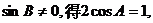 ∴
∴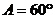 . ………………………………6分
. ………………………………6分
法二 由余弦定理,得 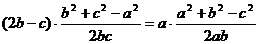 ,
,
∴ 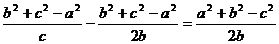 ,
,
∴ 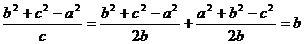 ,
,
∴ 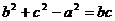 .于是由
.于是由 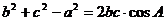 ,
,
得 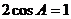 ,∴
,∴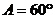 .
.
(2)由已知,得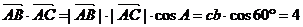 ,
,
∴ 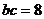 ………………………………9分
………………………………9分
∴ 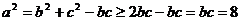 ,即
,即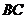 的最小值为
的最小值为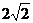 .
.
………………………………12分
DCBA ADBA CDCB
22.(本小题满分12分)已知二次函数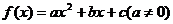 的导函数为
的导函数为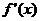 ,且
,且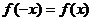 ,
,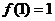 ,
,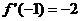 .数列
.数列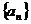 满足
满足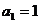 ,且当
,且当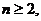
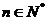 时,
时,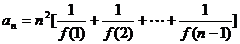 .
.
(1)求函数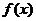 的解析式;
的解析式;
(2) 求证: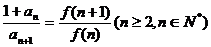 ;
(3)求证:
;
(3)求证: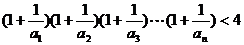 .
.
绵阳市高中2009级第二次诊断性考试
数学(文科)参考解答及评分标准
21. (本小题满分12分)已知动点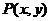 到原点的距离的平方与它到直线
到原点的距离的平方与它到直线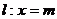 (
(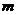 是常数)的距离相等.
是常数)的距离相等.
(1)求动点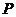 的轨迹方程
的轨迹方程 ;
(2) 就
;
(2) 就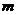 的不同取值讨论方程
的不同取值讨论方程 的图形.
的图形.
20. (本小题满分12分)已知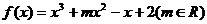 .
.
(1) 如果函数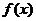 的单调递减区间为
的单调递减区间为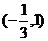 ,求函数
,求函数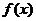 的解析式;
(2)若
的解析式;
(2)若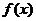 的导函数为
的导函数为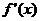 ,对任意
,对任意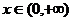 ,不等式
,不等式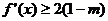 恒成立,求实数
恒成立,求实数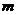 的取值范围.
的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com