5.(2009安徽卷文)考察正方体6个面的中心，从中任意选3个点连成三角形，再把剩下的3个点也连成三角形，则所得的两个三角形全等的概率等于

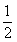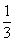　　 A.1　 　 B.　 C. 　 D. 0 .　　　　　

[解析]依据正方体各中心对称性可判断等边三角形有个.由正方体各中心的对称性可得任取三个点必构成等边三角形,故概率为1，选A。.　 　　　

[答案]A

4.(2009安徽卷理)考察正方体6个面的中心，甲从这6个点中任意选两个点连成直线，乙也从这6个点中任意选两个点连成直线，则所得的两条直线相互平行但不重合的概率等于

(A)　　　 (B) 　　　(C)　　 (D)

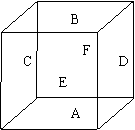[解析] 如图，甲从这6个点中任意选两个点连成直线，乙也从这

6个点中任意选两个点连成直线，共有

种不同取法，其中所得的两条直线相互平行但不重合有

共12对，所以所求概率为，选D

3.(2009山东卷文)在区间上随机取一个数x，的值介于0到之间的概率为(　　　 ).

A.　　　 B.　　　 C.　　　 D. 　　　

[解析]:在区间 上随机取一个数x,即时,要使的值介于0到之间,需使或，区间长度为，由几何概型知的值介于0到之间的概率为.故选A. 　　　

答案:A

[命题立意]:本题考查了三角函数的值域和几何概型问题,由自变量x的取值范围,得到函数值的范围,再由长度型几何概型求得.

2.(2009山东卷理)在区间[-1，1]上随机取一个数x，的值介于0到之间的概率为(　　　 ).

A.　　　 B.　　　 C.　　　 D. 　　　

[解析]:在区间[-1，1]上随机取一个数x,即时,要使的值介于0到之间,需使或∴或，区间长度为，由几何概型知的值介于0到之间的概率为.故选A.

答案:A

[命题立意]:本题考查了三角函数的值域和几何概型问题,由自变量x的取值范围,得到函数值的范围,再由长度型几何概型求得.

1.(2009山东卷理)某工厂对一批产品进行了抽样检测.右图是根据抽样检测后的 　　

产品净重(单位：克)数据绘制的频率分布直方图，其中产品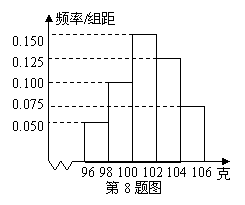

净重的范围是[96，106]，样本数据分组为[96，98)，[98，100),

[100，102)，[102，104),[104，106],已知样本中产品净重小于

100克的个数是36，则样本中净重大于或等于98克并且

小于104克的产品的个数是(　　　　 ).

A.90　 B.75　 C.　 60　　 D.45

[解析]:产品净重小于100克的概率为(0.050+0.100)×2=0.300,

已知样本中产品净重小于100克的个数是36,设样本容量为,

则,所以,净重大于或等于98克并且小于

104克的产品的概率为(0.100+0.150+0.125)×2=0.75,所以样本

中净重大于或等于98克并且小于104克的产品的个数是

120×0.75=90.故选A.

答案:A

[命题立意]:本题考查了统计与概率的知识,读懂频率分布直方图,会计算概率以及样本中有关的数据.

19.(2009重庆卷理)将4名大学生分配到3个乡镇去当村官，每个乡镇至少一名，则不同的分配方案有　　　　　 种(用数字作答)．

[答案]36

[解析]分两步完成：第一步将4名大学生按，2，1，1分成三组，其分法有;第二步将分好的三组分配到3个乡镇，其分法有所以满足条件得分配的方案有

18.(2009重庆卷理)锅中煮有芝麻馅汤圆6个，花生馅汤圆5个，豆沙馅汤圆4个，这三种汤圆的外部特征完全相同。从中任意舀取4个汤圆，则每种汤圆都至少取到1个的概率为(　　 )

A．　 　　 B．　　 　 C．　 　　 D． 　　　　.　 　

[答案]C

[解析]因为总的滔法而所求事件的取法分为三类，即芝麻馅汤圆、花生馅汤圆。豆沙馅汤圆取得个数分别按1.1.2；1，2，1；2，1，1三类，故所求概率为

17.(2009重庆卷理)的展开式中的系数是(　　 )

A．16　　　　　　　　　 B．70　　　　　　　　　 C．560　　　　　　　　 D．1120

[答案]

[解析]设含的为第，

所以，故系数为：，选D。

16.(2009年上海卷理)某学校要从5名男生和2名女生中选出2人作为上海世博会志愿者，若用随机变量表示选出的志愿者中女生的人数，则数学期望____________(结果用最简分数表示). .　 　

[答案]

[解析]可取0，1，2，因此P(＝0)＝， P(＝1)＝，

P(＝2)＝，＝0×＝

15.(2009全国卷Ⅱ理)的展开式中的系数为　　　 6　　　　　 。

解：，只需求展开式中的含项的系数：