
题组一
2009年联考题
13.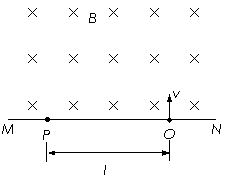 (05·全国 Ⅲ·23) ( 16 分)图中MN表示真空室中垂直于纸面的平板,
(05·全国 Ⅲ·23) ( 16 分)图中MN表示真空室中垂直于纸面的平板,
它的一侧有匀强磁场,磁场方向垂直纸面向里,磁感应强度大小为
B 。一带电粒子从平板上的狭缝O处以垂直于平板的初速v射入磁
场区域,最后到达平板上的P 点。已知B 、v以及P 到O的距离l .
不计重力,求此粒子的电荷q与质量m 之比。
答案: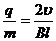
12.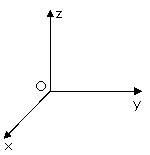 (05·全国Ⅱ·24)在同时存在匀强电场和匀强磁场的空间中取正交坐标系Oxyz(z轴正方向竖直向上),如图所示。已知电场方向沿z轴正方向,场强大小为E;磁场方向沿y轴正方向,磁感应强度的大小为B;重力加速度为g。问:一质量为m、带电量为+q的从原点出发的质点能否在坐标轴(x,y,z)上以速度v做匀速运动?若能,m、q、E、B、v及g应满足怎样的关系?若不能,说明理由。
(05·全国Ⅱ·24)在同时存在匀强电场和匀强磁场的空间中取正交坐标系Oxyz(z轴正方向竖直向上),如图所示。已知电场方向沿z轴正方向,场强大小为E;磁场方向沿y轴正方向,磁感应强度的大小为B;重力加速度为g。问:一质量为m、带电量为+q的从原点出发的质点能否在坐标轴(x,y,z)上以速度v做匀速运动?若能,m、q、E、B、v及g应满足怎样的关系?若不能,说明理由。
答案:已知带电质点受到的电场力为qE ,方向沿z轴正方向;质点受到的重力为mg,沿z轴的负方向。
假设质点在x轴上做匀速运动,则它受的洛伦兹力必沿z轴正方向(当 沿x轴正方向)或沿z轴负方向(当
沿x轴正方向)或沿z轴负方向(当 沿x轴负方向),要质点做匀速运动必分别有
沿x轴负方向),要质点做匀速运动必分别有
q B+qE=mg
①
B+qE=mg
①
或qE= q B+mg ②
B+mg ②
假设质点在y轴上做匀速运动,即无论沿y轴正方向还是负方向,洛伦兹力都为O,要质点做匀速运动必有qE=mg ③
假设质点在z轴上做匀速运动,则它受洛伦兹力必平行于x轴,而电场力和重力都平行于z轴,三力的合力不可能为0,与假设矛盾,故质点不可能在z轴上做匀速运动。
综上所述:液滴能射出,
K应满足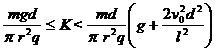

(2)B=B0+Kt
当液滴从两板中点射出进,满足条件一的情况,则
用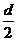 替代⑧式中的d
替代⑧式中的d
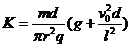
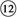
即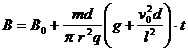

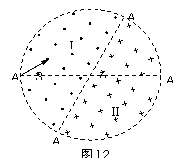
11.(05·广东物理·16)如图12所示,在一个圆形区域内,两个方向相
反且都垂直于纸面的匀强磁场分布在以直径A2A4为边界的两个半圆形区域Ⅰ、
Ⅱ中,A2A4与A1A3的夹角为60º。一质量为m、带电量为+q的粒子以某一速
度从Ⅰ区的边缘点A1处沿与A1A3成30º角的方向射入磁场,随后该粒子以垂
直于A2A4的方向经过圆心O进入Ⅱ区,最后再从A4处射出磁场。已知该
粒子从射入到射出磁场所用的时间为t,求Ⅰ区和Ⅱ区中磁感应强
度的大小(忽略粒子重力)。
答案:设粒子的入射速度为v,已知粒子带正电,故它在磁场中先顺时针做圆周运动,再逆时针做圆周运动,最后从A4点射出,用B1、B2、R1、R 2、T1、T 2分别表示在磁场Ⅰ区Ⅱ磁感应强度、轨道半径和周期
 ①
①
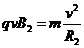 ②
②
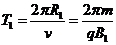 ③
③
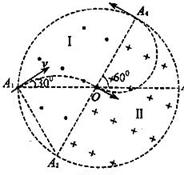
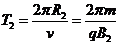 ④
④
设圆形区域的半径为r,如图所示,已知带电粒子过圆心且垂直A3A4进入Ⅱ区磁场,连接A1A2,△A1OA2为等边三角形,A2为带电粒子在Ⅱ区磁场中运动轨迹的圆心,其半径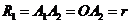 ⑤
⑤
圆心角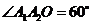 ,带电粒子在Ⅰ区磁场中运动的时间为
,带电粒子在Ⅰ区磁场中运动的时间为
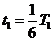 ⑥
⑥
带电粒子在Ⅱ区磁场中运动轨迹的圆心在OA4的中点,即
R=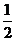 r ⑦
r ⑦
在Ⅱ区磁场中运动时间为
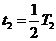 ⑧
⑧
带电粒子从射入到射出磁场所用的总时间
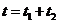 ⑨
⑨
由以上各式可得
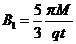 ⑩
⑩
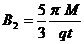

液滴不发生偏转,做匀速直线运动,此时 a=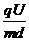 -g=0 ⑨
-g=0 ⑨
由②③⑨得 K2=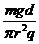 ⑩
⑩
液滴能射出,必须满足K ≥K2
液滴向上偏转,做类似平抛运动
y=  ⑥
⑥
当液滴刚好能射出时:
有 l=v0t t=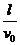 y=d
y=d
故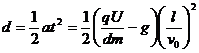 ⑦
⑦
由②③⑦得 K1=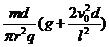 ⑧
⑧
要使液滴能射出,必须满足 y<d 故 K<K1
10. (05·广东物理·17)如图13所示,一半径为r的圆形导线框内有一匀强磁场,磁场方向垂直于
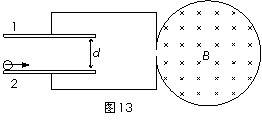 导线框所在平面,导线框的左端通过导线接一对水平放置的平行金属
导线框所在平面,导线框的左端通过导线接一对水平放置的平行金属
板,两板间的距离为d,板长为L,t=0时,磁场的磁感应强度B
从B0开始均匀增大,同时,在板2的左端且非常靠近板2的位置
有一质量为m、带电量为-q的液滴以初速度v0水平向右射入两板间,
该液滴可视为质点。
⑴要使该液滴能从两板间射出,磁感应强度随时间的变化率K应满足什么条件?
⑵要使该液滴能从两板间右端的中点射出,磁
感应强度B与时间t应满足什么关系?
答案:(1)由题意可知:板1为正极,板2为负极 ①
两板间的电压U=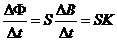 ②
②
而:S=πr2 ③
带电液滴受的电场力:F=qE=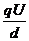 ④
④
故:F-mg=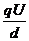 -mg=ma
-mg=ma
a=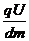 -g
⑤
-g
⑤
讨论:
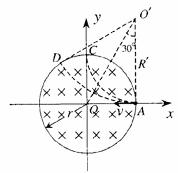
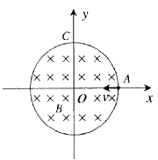
9.(06·天津·24)在以坐标原点O为圆心、半径为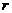 的圆形区域内,存在磁感应强度大小为B、方向垂直于纸面向里的匀强磁场,如图所示。一个不计重力的带电粒子从磁场边界与
的圆形区域内,存在磁感应强度大小为B、方向垂直于纸面向里的匀强磁场,如图所示。一个不计重力的带电粒子从磁场边界与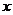 轴的交点A处以速度
轴的交点A处以速度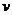 沿
沿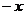 方向射入磁场,它恰好从磁场边界与
方向射入磁场,它恰好从磁场边界与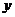 轴的交点C处沿
轴的交点C处沿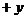 方向飞出。
方向飞出。
(1)请判断该粒子带何种电荷,并求出其比荷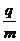 ;
;
(2)若磁场的方向和所在空间范围不变,而磁感应强度的大小变为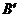 ,该粒子仍从A处以相同的速度射入磁场,但飞出磁场时的速度方向相对于入射方向改变了
,该粒子仍从A处以相同的速度射入磁场,但飞出磁场时的速度方向相对于入射方向改变了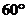 角,求磁感应强度
角,求磁感应强度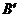 多大?此次粒子在磁场中运动所用时间
多大?此次粒子在磁场中运动所用时间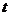 是多少?
是多少?
答案(1)由粒子的飞行轨迹,利用左手定则可知,该粒子带负电荷。
 粒子由A点射入,由C点飞出,其速度方向改变了90°,则粒子轨迹半径
粒子由A点射入,由C点飞出,其速度方向改变了90°,则粒子轨迹半径
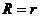 ①
①
又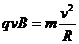 ②
②
则粒子的比荷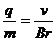 ③
③
(2)粒子从D点飞出磁场速度方向改变了60°角,故AD弧所对圆心角为60°,粒子做圆周运动的半径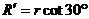 =
=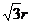 ④
④
又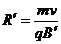 ⑤ 所以
⑤ 所以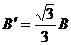 ⑥
⑥
粒子在磁场中飞行时间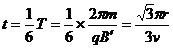 ⑦
⑦
8. (06·全国Ⅱ·25)(20分)如图所示,在
(06·全国Ⅱ·25)(20分)如图所示,在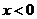 与
与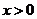 的区域中,存在磁感应强度大小分别为
的区域中,存在磁感应强度大小分别为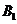 与
与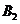 的匀强磁场,磁场方向均垂直于纸面向里,且
的匀强磁场,磁场方向均垂直于纸面向里,且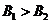 . 一个带负电荷的粒子从坐标原点
. 一个带负电荷的粒子从坐标原点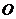 以速度
以速度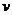 沿
沿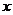 轴负方向射出,要使该粒子经过一段时间后又经过
轴负方向射出,要使该粒子经过一段时间后又经过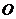 点,
点,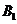 与
与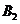 的比值应满足什么条件?
的比值应满足什么条件?
 解:粒子在整个过程中的速度大小恒为
解:粒子在整个过程中的速度大小恒为 ,交替地在
,交替地在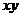 平面内
平面内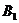 与
与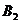 磁场区域中做匀速圆周运动,轨道都是半个圆周.设粒子的质量和电荷量的大小分别为
磁场区域中做匀速圆周运动,轨道都是半个圆周.设粒子的质量和电荷量的大小分别为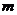 和
和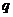 ,圆周运动的半径分别为
,圆周运动的半径分别为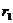 和
和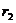 ,有
,有
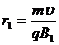 ①
①
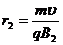 ②
②
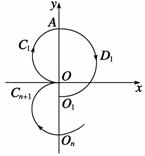
现分析粒子运动的轨迹.如图所示,在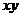 平面内,粒子先沿半径为
平面内,粒子先沿半径为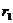 的半圆
的半圆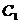 运动至
运动至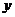 轴上离
轴上离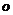 点距离为
点距离为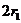 的
的 点,接着沿半径为
点,接着沿半径为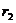 的半圆
的半圆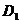 运动至
运动至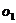 点,
点,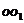 的距离
的距离
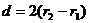 ③
③
此后,粒子每经历一次“回旋”(即从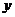 轴出发沿半径为
轴出发沿半径为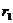 的半圆和半径为
的半圆和半径为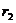 的半圆回到原点下方的
的半圆回到原点下方的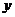 轴),粒子的
轴),粒子的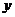 坐标就减小
坐标就减小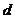 .设粒子经过
.设粒子经过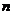 次回旋后与
次回旋后与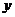 轴交于
轴交于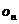 点,若
点,若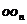 即
即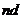 满足
满足
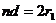 ④
④
则粒子再经过半圆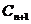 就能经过原点,式中
就能经过原点,式中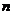 =1,2,3,……为回旋次数.
=1,2,3,……为回旋次数.
由③④式解得
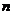 =1,2,3,…… ⑤
=1,2,3,…… ⑤
联立①②⑤式可得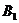 、
、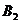 应满足的条件:
应满足的条件:
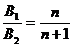
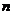 =1,2,3,…… ⑥
=1,2,3,…… ⑥
7.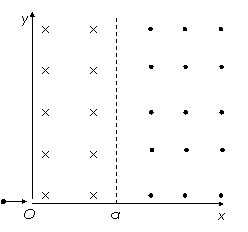 (07·全国理综Ⅰ·25)两平面荧光屏互相垂直放置,在两屏内分别取垂直于两屏交线的直线为x轴和y轴,交点O为原点,如图所示,在y>0,0<x<a的区域有垂直于纸面向里的匀强磁场,在y>0,x>a的区域有垂直于纸面向外的匀强磁场,两区域内的磁感应强度大小均为B。在O点有一处小孔,一束质量为m、带电量为q(q>0)的粒子沿x轴经小孔射入磁场,最后扎在竖直和水平荧光屏上,使荧光屏发亮。入射粒子的速度可取从零到某一最大值之间的各种数值。已知速度最大的粒子在0<x<a的区域中运动的时间与在x>a的区域中运动的时间之比为2∶5,在磁场中运动的总时间为7T/12,其中T为该粒子在磁感应强度为B的匀强磁场中作圆周运动的周期。试求两个荧光屏上亮线的范围(不计重力的影响)。
(07·全国理综Ⅰ·25)两平面荧光屏互相垂直放置,在两屏内分别取垂直于两屏交线的直线为x轴和y轴,交点O为原点,如图所示,在y>0,0<x<a的区域有垂直于纸面向里的匀强磁场,在y>0,x>a的区域有垂直于纸面向外的匀强磁场,两区域内的磁感应强度大小均为B。在O点有一处小孔,一束质量为m、带电量为q(q>0)的粒子沿x轴经小孔射入磁场,最后扎在竖直和水平荧光屏上,使荧光屏发亮。入射粒子的速度可取从零到某一最大值之间的各种数值。已知速度最大的粒子在0<x<a的区域中运动的时间与在x>a的区域中运动的时间之比为2∶5,在磁场中运动的总时间为7T/12,其中T为该粒子在磁感应强度为B的匀强磁场中作圆周运动的周期。试求两个荧光屏上亮线的范围(不计重力的影响)。
解:粒子在磁感应强度为B的匀强磁场中运动的半径为:
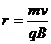
速度小的粒子将在x<a的区域走完半圆,射到竖直屏上。半圆的直径在y轴上,半径的范围从0到a,屏上发亮的范围从0到2a。
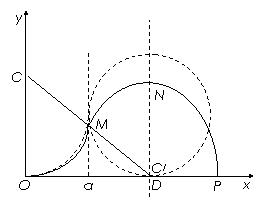 轨道半径大于a的粒子开始进入右侧磁场,考虑r=a的极限情况,这种粒子在右侧的圆轨迹与x轴在D点相切(虚线),OD=2a,这是水平屏上发亮范围的左边界。
轨道半径大于a的粒子开始进入右侧磁场,考虑r=a的极限情况,这种粒子在右侧的圆轨迹与x轴在D点相切(虚线),OD=2a,这是水平屏上发亮范围的左边界。
速度最大的粒子的轨迹如图中实线所示,它由两段圆弧组成,圆心分别为C和C/,C在y轴上,由对称性可知C/在x=2a直线上。
设t1为粒子在0<x<a的区域中运动的时间,t2为在x>a的区域中运动的时间,由题意可知 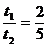
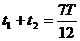
解得: 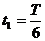
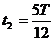
由两式和对称性可得:
∠OCM=60°
∠MC/N=60°
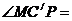 360°
360°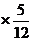 =150°
=150°
所以 ∠NC/P=150°-60°=90°
R=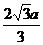
由图可知OP=2a+R,因此水平荧光屏发亮范围的右边界坐标为
X=2(1+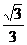 )a
)a
即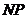 为
为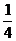 圆周,因此,圆心C/在x轴上。
圆周,因此,圆心C/在x轴上。
设速度为最大值粒子的轨道半径为R,由直角ΔCOC/可得
2Rsin60°=2a
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com