
4、设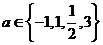 ,则使函数
,则使函数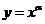 的定义域为R且为奇函数的所有
的定义域为R且为奇函数的所有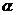 值为
值为
2、在R上定义的函数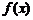 是偶函数,且
是偶函数,且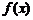
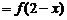 .若
.若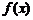 在区间
在区间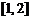 上是减函数,则
上是减函数,则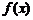
在区间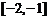 上是 函数,在区间
上是 函数,在区间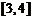 上是
函数
上是
函数
1、 ,
,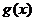 是定义在R上的函数,
是定义在R上的函数,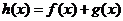 ,则“
,则“ ,
,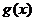 均为偶函数”是“
均为偶函数”是“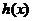 为偶函数”的
条件
为偶函数”的
条件
4.判断下列函数的奇偶性:
①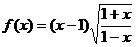 ,②
,②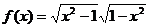 ,③
,③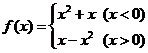
典型例题
例1.已知函数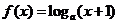 ,
,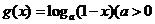 ,且
,且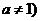
(1)
求函数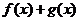 定义域
定义域
(2)
判断函数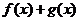 的奇偶性,并说明理由.
的奇偶性,并说明理由.
变式1:已知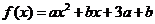 是偶函数,定义域为
是偶函数,定义域为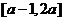 .则
.则 ,
,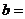
变式2:函数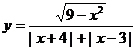 的图象关于 ( )
的图象关于 ( )
A.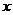 轴对称
B.
轴对称
B.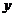 轴对称 C.原点对称 D.直线
轴对称 C.原点对称 D.直线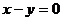 对称
对称
变式3:若函数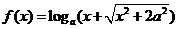 是奇函数,则
是奇函数,则
变式4:函数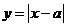 的图象关于直线
的图象关于直线 对称.则
对称.则
变式5:函数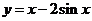 在
在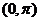 上的单调递增区间为
上的单调递增区间为
例2、已知函数 是偶函数,而且在
是偶函数,而且在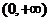 上是减函数,判断
上是减函数,判断 在
在 上是增函数还是减函数,并证明你的判断.
上是增函数还是减函数,并证明你的判断.
变式1:下列函数中,在其定义域内既是奇函数又是减函数的是
A. 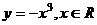 B.
B. 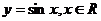 C.
C. 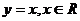 D.
D.
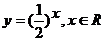
变式2:函数 是R上的偶函数,且在
是R上的偶函数,且在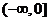 上是增函数,若
上是增函数,若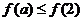 ,则实数
,则实数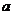 的取值范围是
的取值范围是
设计意图:考察函数奇偶性与单调性的关系
例3、已知函数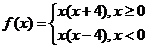 ,求
,求 ,
,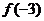 ,
,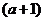 的值
的值
变式1:设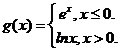 则
则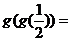 __________
__________
变式2:已知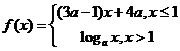 是
是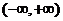 上的减函数,那么
上的减函数,那么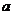 的取值范围是
的取值范围是
例4、设函数f(x)的定义域是N*,且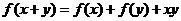 ,
,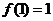 ,则f(25)=
,则f(25)=
变式1:设函数 定义在R上,对任意实数m、n,恒有
定义在R上,对任意实数m、n,恒有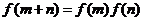 且当
且当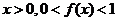
(1)求证:f(0)=1,且当x<0时,f(x)>1;
(2)求证:f(x)在R上递减;
(3)设集合A={(x,y)|f(x2)·f(y2)>f(1)},B={(x,y)|f(ax-y+2)=1,
a∈R},若A∩B=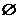 ,求a的取值范围.
,求a的取值范围.
实战演练
3.已知函数f (x), g (x)在 R上是增函数,求证:f [g (x)]在 R上也是增函数。
2.函数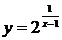 在定义域上的单调性为
在定义域上的单调性为
(A)在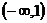 上是增函数,在
上是增函数,在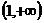 上是增函数;(B)减函数;
上是增函数;(B)减函数;
(C)在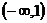 上是减函数,在
上是减函数,在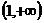 上是减函数;(D)增函数
上是减函数;(D)增函数
1.讨论函数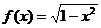 的单调性。
的单调性。
4. 奇函数
⑴奇函数: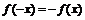 .设(
.设(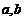 )为奇函数上一点,则(
)为奇函数上一点,则(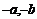 )也是图象上一点.
)也是图象上一点.
⑵奇函数的判定:两个条件同时满足①定义域一定要关于原点对称,例如: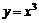 在
在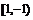 上不是奇函数.②满足
上不是奇函数.②满足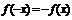 ,或
,或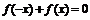 ,若
,若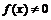 时,
时,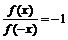 .
.
注:函数定义域关于原点对称是判断函数奇偶性的必要条件,在利用定义判断时,应在化简解析式后进行,同时灵活运用定义域的变形,如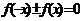 ,
,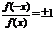 (f(x)≠0)
(f(x)≠0)
课前练习
3.偶函数
⑴偶函数: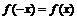 .设(
.设(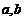 )为偶函数上一点,则(
)为偶函数上一点,则(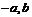 )也是图象上一点.
)也是图象上一点.
⑵偶函数的判定:两个条件同时满足
①
定义域一定要关于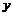 轴对称,例如:
轴对称,例如: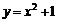 在
在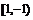 上不是偶函数.
上不是偶函数.
②
满足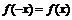 ,或
,或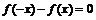 ,若
,若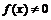 时,
时,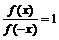 .
.
2、单调性:研究函数的单调性应结合函数单调区间,单调区间应是定义域的子集。
判断函数单调性的方法:
① 定义法(作差比较和作商比较);
② 图象法;
③ 单调性的运算性质(实质上是不等式性质);
④ 复合函数单调性判断法则;
⑤ 导数法(适用于多项式函数)
注:函数单调性是函数性质中最活跃的性质,它的运用主要体现在不等式方面,如比较大小,解抽象函数不等式等。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com