2009.3
命题:余绍安(天台中学) 徐跃文(温岭中学)
审题:王建华(黄岩中学)
注意事项:
1.
本卷共4页,三大题,22小题,满分150分,考试时间120分钟;
2.
用蓝、黑色水笔或圆珠笔书写答案,考试结束只需将答案纸交回.
参考公式:
如果事件A,B互斥,那么
棱柱的体积公式
 V=Sh
V=Sh
如果事件A,B相互独立,那么
其中S表示棱柱的底面积,h表示棱柱的高
 棱锥的体积公式
棱锥的体积公式
在n次独立重复试验中事件A恰好
V= Sh
Sh
发生k次的概率是 ,
其中S表示棱锥的底面积,h表示棱锥的高
,
其中S表示棱锥的底面积,h表示棱锥的高
其中p表示在一次试验中事件A发生的概率
棱台的体积公式
球的表面积公式 

球的体积公式  其中S1, S2分别表示棱台的上底、下底面积,
其中S1, S2分别表示棱台的上底、下底面积,
其中R表示球的半径
h表示棱台的高
一.选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一 项是符合题目要求的.
试题详情
试题详情
试题详情
试题详情
3. 现要完成下列3项抽样调查:
①从10盒酸奶中抽取3盒进行食品卫生检查.
②科技报告厅有32排,每排有40个座位,有一次报告会恰好坐满了听众,报告会结束后,为了听取意见,需要请32名听众进行座谈.
③东方中学共有160名教职工,其中一般教师120名,行政人员16名,后勤人员24名.为了了解教职工对学校在校务公开方面的意见,拟抽取一个容量为20的样本.较为合理的抽样方法是
(A) ①简单随机抽样,②系统抽样,③分层抽样.
(B) ①简单随机抽样,②分层抽样,③系统抽样.
(C) ①系统抽样,②简单随机抽样,③分层抽样.
试题详情
 (D) ①分层抽样,②系统抽样,③简单随机抽样.
(D) ①分层抽样,②系统抽样,③简单随机抽样.
试题详情
4.已知函数 ,
,
试题详情
且函数的图象如图所示,则点 的坐标是
的坐标是
试题详情
(A)  (B)
(B)
试题详情
(C) (D)
(D)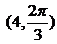
试题详情
 5.根据右边程序框图,若输出
5.根据右边程序框图,若输出 的值是4,
的值是4,
试题详情
则输入的实数 的值为
的值为
试题详情
(A)
试题详情
(B)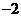
试题详情
(C)  或
或
试题详情
(D)  或
或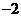
试题详情
试题详情
试题详情
(A)4 (B) 
试题详情
(C)  (D)
(D) 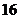
试题详情
7.设直线 与平面
与平面 相交但不垂直,则下列说法中正确的是
相交但不垂直,则下列说法中正确的是
试题详情
(A) 在平面 内有且只有一条直线与直线
内有且只有一条直线与直线 垂直
垂直
试题详情
(B) 过直线 有且只有一个平面与平面
有且只有一个平面与平面 垂直
垂直
试题详情
(C) 与直线 垂直的直线不可能与平面
垂直的直线不可能与平面 平行
平行
试题详情
(D) 与直线 平行的平面不可能与平面
平行的平面不可能与平面 垂直
垂直
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
(A) ①③ (B) ③④ 学 (C) ①②③ (D) ①③④
学 (C) ①②③ (D) ①③④ 学科
学科
试题详情
二.填空题:本大题共7小题,每小题4分,共28分.
试题详情
试题详情
试题详情
试题详情
14.一几何体的三视图如下图,则它的体积为 ▲ .
试题详情
试题详情
试题详情
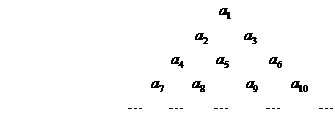
则此数阵中第20行从左到右的第10个数是 ▲ .
试题详情
试题详情
试题详情
三.解答题:本大题共5小题,解答应写出文字说明、证明过程或演算步骤.
试题详情
(Ⅰ)求角 的大小;
的大小;
试题详情
(Ⅱ)求 的取值范围.
的取值范围.
试题详情
19.(本题满分14分)体育课进行篮球投篮达标测试,规定:每位同学有5次投篮机会,若投中3次则“达标”;为节省测试时间,同时规定:若投篮不到5次已达标,则停止投篮;若后面投篮全中,也不能达标(例如前3次都未投中等情形),则停止投篮.同学甲投篮命中率为 且每次投篮互不影响.
且每次投篮互不影响.
(Ⅰ)求同学甲恰好投4次达标的概率;
(Ⅱ)设测试中甲投篮次数记为ξ,求ξ的分布列及数学期望Eξ.
试题详情
试题详情
(Ⅰ)求证: ⊥平面
⊥平面 ;
;
试题详情
(Ⅱ)求二面角 的正切值;
的正切值;
试题详情
(Ⅲ)试确定点 的位置,使直线
的位置,使直线
试题详情
试题详情
试题详情
(Ⅰ)求过点 且焦点在
且焦点在 轴上的抛物线的标准方程;
轴上的抛物线的标准方程;
试题详情
(Ⅱ)过点(1,0)作直线 与(Ⅰ)中的抛物线相交于
与(Ⅰ)中的抛物线相交于
 两点,问是否存在定点
两点,问是否存在定点 使
使 为常数?若存在,求出点
为常数?若存在,求出点 的坐标及常数;若不存在,请说明理由.
的坐标及常数;若不存在,请说明理由.
试题详情
22.(本题满分15分)已知函数 ,点
,点 .
.
试题详情
试题详情
试题详情
(Ⅲ)若 ,函数
,函数 在
在 和
和 处取得极值,且
处取得极值,且 ,
, 是坐标原点,证明:直线
是坐标原点,证明:直线 与直线
与直线 不可能垂直.
不可能垂直.
试题详情
一、选择题(每小题5分,共50分)

二、填空题(每小题4分,共28分)

三、解答题
18.解:(Ⅰ)由已有



(4分)

(6分)
(Ⅱ)由(1) 且
且 (8分)
(8分)
所以 (10分)
(10分)
 (12分)
(12分)

 (14分)
(14分)
19.解:(Ⅰ)同学甲同学恰好投4次达标的概率 (4分)
(4分)
(Ⅱ) 可取的值是
可取的值是
 (6分)
(6分)
 (8分)
(8分)
 (10分)
(10分)
 的分布列为
的分布列为

3
4
5



(12分)
所以 的数学期望为
的数学期望为 (14分)
(14分)
20.解:(Ⅰ)∵PA⊥底面ABCD,BC 平面AC,∴PA⊥BC
平面AC,∴PA⊥BC
∵∠ACB=90°,∴BC⊥AC,又PA∩AC=A,∴BC⊥平面PAC
(4分)
(Ⅱ)取CD的中点E,则AE⊥CD,∴AE⊥AB,又PA⊥底面ABCD,∴PA⊥AE
建立如图所示空间直角坐标系,则
A(0,,0,0),P(0,0, ),C(
),C( ,0),D(
,0),D( ,0)
,0)

 ,
, ,
, (6分)
(6分)
易求 为平面PAC的一个法向量.
为平面PAC的一个法向量.
 为平面PDC的一个法向量
(9分)
为平面PDC的一个法向量
(9分)
∴cos
故二面角D-PC-A的正切值为2. (11分)
(Ⅲ)设 ,则
,则
 ,
,
解得点 ,即
,即 (13分)
(13分)
由 得
得 (不合题意舍去)或
(不合题意舍去)或
所以当 为
为 的中点时,直线
的中点时,直线 与平面
与平面 所成角的正弦值为
所成角的正弦值为 (15分)
(15分)
21.解:(Ⅰ)设直线 的方程为:
的方程为:
由 得
得 ,所以
,所以 的方程为
的方程为 (4分)
(4分)
由 得
得 点的坐标为
点的坐标为 .
.
可求得抛物线的标准方程为 .
(6分)
.
(6分)
(Ⅱ)设直线 的方程为
的方程为 ,代入抛物线方程并整理得
,代入抛物线方程并整理得 (8分)
(8分)
设 则
则
设 ,则
,则



 (11分)
(11分)
当 时上式是一个与
时上式是一个与 无关的常数.
无关的常数.
所以存在定点 ,相应的常数是
,相应的常数是 .
(14分)
.
(14分)
22.解:(Ⅰ)当 时
时 (2分)
(2分)
 在
在 上递增,在
上递增,在 上递减
上递减
所以 在0和2处分别达到极大和极小,由已知有
在0和2处分别达到极大和极小,由已知有
 且
且 ,因而
,因而 的取值范围是
的取值范围是 .
(4分)
.
(4分)
(Ⅱ)当 时,
时, 即
即
