科目:czsx 来源:2015-2016学年陕西省八年级上学期第一次月考数学试卷(解析版) 题型:选择题
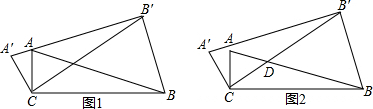
如图,在Rt△ABC中,∠ACB=90°,AB=6,若以AB边和BC斌向外作等腰直角三角形AFC和等腰直角三角形BEC.若△BEC的面积为S1,△AFC的面积为S2,则S1+S2=( )

A.4 B.9 C.18 D.36
科目:czsx 来源: 题型:填空题
 如图,在Rt△ABC中,∠ACB=90°,AB=5,AC=3,点D是BC上一动点,连结AD,将△ACD沿AD折叠,点C落在点C′,连结C′D交AB于点E,连结BC′.当△BC′D是直角三角形时,DE的长为$\frac{3}{2}$或$\frac{3}{4}$.
如图,在Rt△ABC中,∠ACB=90°,AB=5,AC=3,点D是BC上一动点,连结AD,将△ACD沿AD折叠,点C落在点C′,连结C′D交AB于点E,连结BC′.当△BC′D是直角三角形时,DE的长为$\frac{3}{2}$或$\frac{3}{4}$. 科目:czsx 来源: 题型:选择题
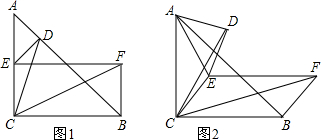
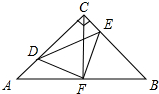 如图,在等腰Rt△ABC中,∠ACB=90°,AC=CB=4,F是AB边上的中点,点D、E分别在AC、BC边上运动(点D不与点A,C重合),且始终保持AD=CE.连接DE、DF、EF.在此运动变化的过程中,有下列结论:
如图,在等腰Rt△ABC中,∠ACB=90°,AC=CB=4,F是AB边上的中点,点D、E分别在AC、BC边上运动(点D不与点A,C重合),且始终保持AD=CE.连接DE、DF、EF.在此运动变化的过程中,有下列结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
科目:czsx 来源: 题型:填空题
 如图,在Rt△ABC中,∠ACB=90°,AB=5,cosB=$\frac{3}{5}$,现作如下操作:将△ACB沿直线AC翻折,然后再放大得到△A′CB′,联结A′B,如果△AA′B是等腰三角形,那么B′C的长是$\frac{27}{4}$.
如图,在Rt△ABC中,∠ACB=90°,AB=5,cosB=$\frac{3}{5}$,现作如下操作:将△ACB沿直线AC翻折,然后再放大得到△A′CB′,联结A′B,如果△AA′B是等腰三角形,那么B′C的长是$\frac{27}{4}$. 科目:czsx 来源: 题型:解答题
科目:czsx 来源: 题型:

科目:czsx 来源: 题型:
如图2318,在直角三角形ABC中,∠ACB=90°,AC=BC=10,将△ABC绕点B沿顺时针方向旋转90°得到△A1BC1.
(1)线段A1C1的长度是________,∠CBA1的度数是________;
(2)连接CC1,求证:四边形CBA1C1是平行四边形.

科目:czsx 来源: 题型:
如图,在直角三角形ABC中,∠ACB=90°,点O在AB上,且CA=CO,若将直角三角形ABC绕着点A顺时针旋转,得到直角三角形AED,B、C的对应点分别为E、D,且点D落在CO的延长线上,连接BE交CO的延长线于点F,若CA=6,AB=18,则BF的长为 .


科目:czsx 来源: 题型:解答题
 如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.
如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.科目:czsx 来源: 题型:填空题
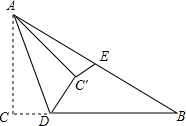 如图,在△ABC中,∠ACB=90°,AC=2,BC=4,E为边AB的中点,点D是BC边上的动点,把△ACD沿AD翻折,点C落在C′处,若△AC′E是直角三角形,则CD的长为2或$\frac{2}{3}$.
如图,在△ABC中,∠ACB=90°,AC=2,BC=4,E为边AB的中点,点D是BC边上的动点,把△ACD沿AD翻折,点C落在C′处,若△AC′E是直角三角形,则CD的长为2或$\frac{2}{3}$. 科目:czsx 来源: 题型:解答题
 如图,在等腰直角三角形ABC中,∠ACB=90°,点D在边AB上,连接CD,过点A,C分别作AB,CD的垂线,两垂线交于点E,连接DE.
如图,在等腰直角三角形ABC中,∠ACB=90°,点D在边AB上,连接CD,过点A,C分别作AB,CD的垂线,两垂线交于点E,连接DE.科目:czsx 来源: 题型:解答题
科目:gzsx 来源: 题型:解答题
 如图,直三棱柱ABC-A1B1C1中,底面是等腰直角三角形,∠ACB=90°,侧棱AA1=2,D、E分别是CC1与A1B的中点,点E在平面ABD上的射影是△ABD的垂心G.
如图,直三棱柱ABC-A1B1C1中,底面是等腰直角三角形,∠ACB=90°,侧棱AA1=2,D、E分别是CC1与A1B的中点,点E在平面ABD上的射影是△ABD的垂心G.科目:czsx 来源: 题型:解答题