
题目列表(包括答案和解析)
15.将杨辉三角中的每一个数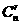 都换成
都换成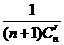 ,就得到一个如右图所示的分数三角形,成为莱布尼茨三角形,从莱布尼茨三角形可看出
,就得到一个如右图所示的分数三角形,成为莱布尼茨三角形,从莱布尼茨三角形可看出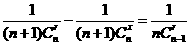 ,其中
,其中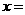 r+1 。令
r+1 。令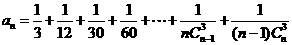 ,则
,则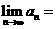 。
。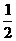
14.某工程队有6项工程需要单独完成,其中工程乙必须在工程甲完成后才能进行,工程丙必须在工程乙完成后才能进行,有工程丁必须在工程丙完成后立即进行。那么安排这6项工程的不同排法种数是 20 。(用数字作答)
13.已知直线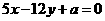 与圆
与圆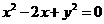 相切,则
相切,则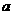 的值为 -18或8 。
的值为 -18或8 。
12.接种某疫苗后,出现发热反应的概率为0.80,现有5人接种了该疫苗,至少有3人出现发热反应的概率为 0.94 。(精确到0.01)
11.设 为实数,且
为实数,且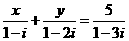 ,则
,则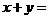 4 。
4 。
10.关于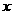 的方程
的方程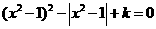 ,给出下列四个命题: ( A )
,给出下列四个命题: ( A )
①存在实数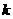 ,使得方程恰有2个不同的实根;
,使得方程恰有2个不同的实根;
②存在实数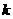 ,使得方程恰有4个不同的实根;
,使得方程恰有4个不同的实根;
③存在实数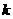 ,使得方程恰有5个不同的实根;
,使得方程恰有5个不同的实根;
④存在实数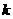 ,使得方程恰有8个不同的实根;
,使得方程恰有8个不同的实根;
其中假命题的个数是
A.0 B.1 C.2 D.3
第Ⅱ卷(非选择题 共100分)
第Ⅱ卷用0.5毫米黑色的签字笔或黑色墨水钢笔直接答在答题卡上。答在试题卷上无效。
9.已知平面区域D由以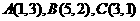 为顶点的三角形内部&边界组成。若在区域D上有无穷多个点
为顶点的三角形内部&边界组成。若在区域D上有无穷多个点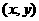 可使目标函数
可使目标函数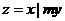 取得最小值,则
取得最小值,则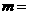 (C )
(C )
A.-2 B.-1 C.1 D.4
8.有限集合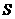 中元素的个数记做
中元素的个数记做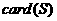 ,设
,设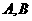 都为有限集合,给出下列命题:
都为有限集合,给出下列命题:
①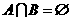 的充要条件是
的充要条件是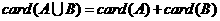 ;
;
②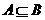 的充要条件是
的充要条件是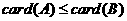 ;
;
③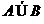 的充要条件是
的充要条件是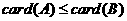 ;
;
④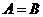 的充要条件是
的充要条件是 ;
;
其中真命题的序号是 ( B )
A.③④ B.①② C.①④ D.②③
7.设过点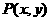 的直线分别与
的直线分别与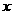 轴的正半轴和
轴的正半轴和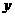 轴的正半轴交于
轴的正半轴交于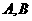 两点,点
两点,点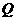 与点
与点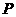 关于
关于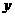 轴对称,
轴对称, 为坐标原点,若
为坐标原点,若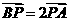 且
且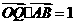 ,则点
,则点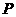 的轨迹方程是 ( D )
的轨迹方程是 ( D )
A.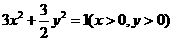 B.
B.
C.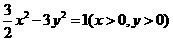 D.
D.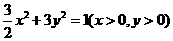
6.关于直线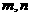 与平面
与平面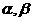 ,有以下四个命题:
,有以下四个命题:
①若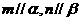 且
且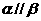 ,则
,则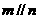 ;
;
②若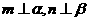 且
且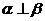 ,则
,则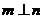 ;
;
③若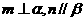 且
且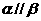 ,则
,则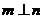 ;
;
④若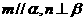 且
且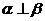 ,则
,则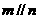 ;
;
其中真命题的序号是 ( D )
A.①② B.③④ C.①④ D.②③
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com