
题目列表(包括答案和解析)
(17)(本大题满分12分)已知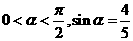
(Ⅰ)求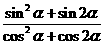 的值;
的值;
(Ⅱ)求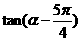 的值。
的值。
解:(Ⅰ)由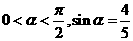 ,得
,得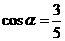 ,所以
,所以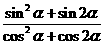 =
=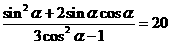 。
。
(Ⅱ)∵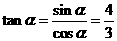 ,∴
,∴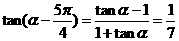 。
。
(18)(本大题满分12分)在添加剂的搭配使用中,为了找到最佳的搭配方案,需要对各种不同的搭配方式作比较。在试制某种牙膏新品种时,需要选用两种不同的添加剂。现有芳香度分别为0,1,2,3,4,5的六种添加剂可供选用。根据试验设计原理,通常首先要随机选取两种不同的添加剂进行搭配试验。
(Ⅰ)求所选用的两种不同的添加剂的芳香度之和等于4的概率;
(Ⅱ)求所选用的两种不同的添加剂的芳香度之和不小于3的概率;
解:设“所选用的两种不同的添加剂的芳香度之和等于4”的事件为A,“所选用的两种不同的添加剂的芳香度之和不小于3”的事件为B
 (Ⅰ)芳香度之和等于4的取法有2种:
(Ⅰ)芳香度之和等于4的取法有2种: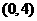 、
、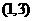 ,故
,故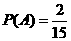 。
。
(Ⅱ)芳香度之和等于1的取法有1种: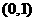 ;芳香度之和等于2的取法有1种:
;芳香度之和等于2的取法有1种: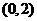 ,故
,故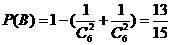 。
。
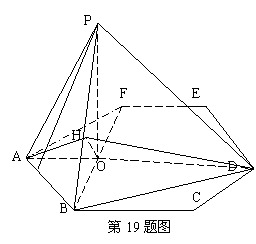
(19)(本大题满分12分)如图,P是边长为1的正六边形ABCDEF所在平面外一点,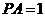 ,P在平面ABC内的射影为BF的中点O。
,P在平面ABC内的射影为BF的中点O。
(Ⅰ)证明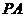 ⊥
⊥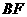 ;
;
(Ⅱ)求面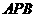 与面
与面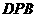 所成二面角的大小。
所成二面角的大小。
解:(Ⅰ)在正六边形ABCDEF中,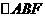 为等腰三角形,
为等腰三角形,
∵P在平面ABC内的射影为O,∴PO⊥平面ABF,∴AO为PA在平面ABF内的射影;∵O为BF中点,∴AO⊥BF,∴PA⊥BF。
(Ⅱ)∵PO⊥平面ABF,∴平面PBF⊥平面ABC;而O为BF中点,ABCDEF是正六边形 ,∴A、O、D共线,且直线AD⊥BF,则AD⊥平面PBF;又∵正六边形ABCDEF的边长为1,∴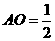 ,
,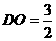 ,
,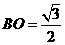 。
。
过O在平面POB内作OH⊥PB于H,连AH、DH,则AH⊥PB,DH⊥PB,所以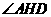 为所求二面角平面角。
为所求二面角平面角。
在 中,OH=
中,OH=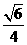 ,
,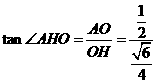 =
=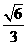 。
。
在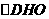 中,
中,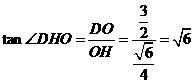 ;
;
而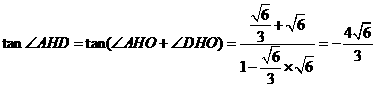
(Ⅱ)以O为坐标原点,建立空间直角坐标系,P(0,0,1),A(0,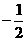 ,0),B(
,0),B(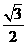 ,0,0),D(0,2,0),∴
,0,0),D(0,2,0),∴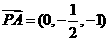 ,
,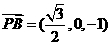 ,
,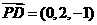
设平面PAB的法向量为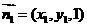 ,则
,则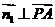 ,
,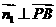 ,得
,得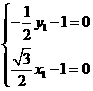 ,
,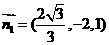 ;
;
设平面PDB的法向量为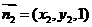 ,则
,则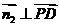 ,
,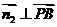 ,得
,得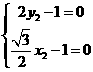 ,
,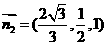 ;
;
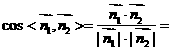
(20)(本大题满分12分)设函数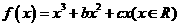 ,已知
,已知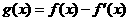 是奇函数。
是奇函数。
(Ⅰ)求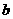 、
、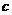 的值。
的值。
(Ⅱ)求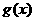 的单调区间与极值。
的单调区间与极值。
证明(Ⅰ)∵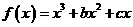 ,∴
,∴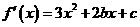 。从而
。从而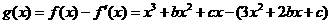 =
=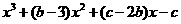 是一个奇函数,所以
是一个奇函数,所以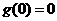 得
得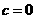 ,由奇函数定义得
,由奇函数定义得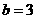 ;
;
(Ⅱ)由(Ⅰ)知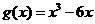 ,从而
,从而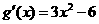 ,由此可知,
,由此可知,
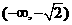 和
和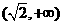 是函数
是函数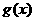 是单调递增区间;
是单调递增区间;
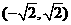 是函数
是函数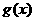 是单调递减区间;
是单调递减区间;
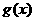 在
在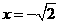 时,取得极大值,极大值为
时,取得极大值,极大值为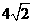 ,
,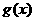 在
在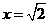 时,取得极小值,极小值为
时,取得极小值,极小值为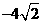 。
。
(21)(本大题满分12分)在等差数列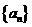 中,
中,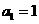 ,前
,前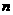 项和
项和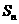 满足条件
满足条件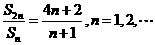 ,
,
(Ⅰ)求数列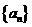 的通项公式;
的通项公式;
(Ⅱ)记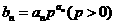 ,求数列
,求数列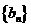 的前
的前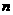 项和
项和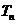 。
。
解:(Ⅰ)设等差数列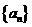 的公差为
的公差为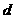 ,由
,由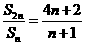 得:
得: ,所以
,所以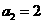 ,即
,即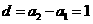 ,又
,又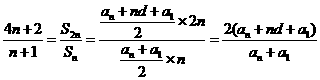 =
=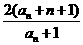 ,所以
,所以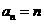 。
。
(Ⅱ)由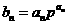 ,得
,得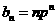 。所以
。所以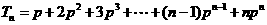 ,
,
当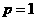 时,
时,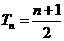 ;
;
当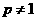 时,
时,
 ,
,

即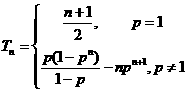 。
。
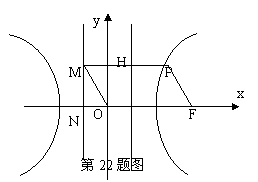
(22)(本大题满分14分)如图,F为双曲线C: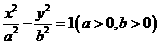 的右焦点。P为双曲线C右支上一点,且位于
的右焦点。P为双曲线C右支上一点,且位于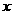 轴上方,M为左准线上一点,
轴上方,M为左准线上一点, 为坐标原点。已知四边形
为坐标原点。已知四边形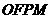 为平行四边形,
为平行四边形,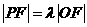 。
。
 (Ⅰ)写出双曲线C的离心率
(Ⅰ)写出双曲线C的离心率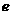 与
与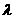 的关系式;
的关系式;
(Ⅱ)当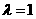 时,经过焦点F且平行于OP的直线交双曲线于A、B点,若
时,经过焦点F且平行于OP的直线交双曲线于A、B点,若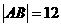 ,求此时的双曲线方程。
,求此时的双曲线方程。
解:∵四边形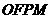 是
是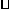 ,∴
,∴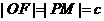 ,作双曲线的右准线交PM于H,则
,作双曲线的右准线交PM于H,则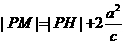 ,又
,又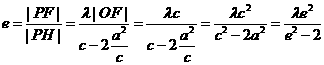 ,
,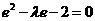 。
。
(Ⅱ)当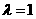 时,
时,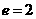 ,
,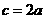 ,
,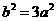 ,双曲线为
,双曲线为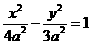 ,设P
,设P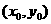 ,则
,则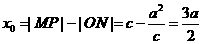 ,
,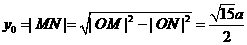 ,所以直线OP的斜率为
,所以直线OP的斜率为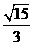 ,则直线AB的方程为
,则直线AB的方程为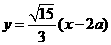 ,代入到双曲线方程得:
,代入到双曲线方程得: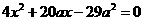 ,
,
又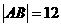 ,由
,由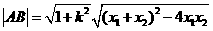 得:
得: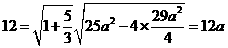 ,解得
,解得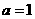 ,则
,则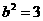 ,所以
,所以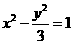 为所求。
为所求。
(13)设常数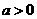 ,
,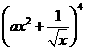 展开式中
展开式中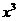 的系数为
的系数为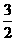 ,则
,则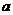 =_____。
=_____。
解: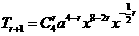 ,由
,由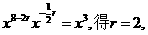
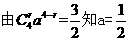 。
。
(14)在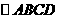 中,
中,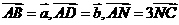 ,M为BC的中点,则
,M为BC的中点,则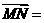 _______。(用
_______。(用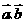 表示)
表示)
解: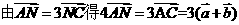 ,
,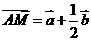 ,所以
,所以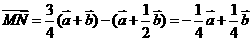 。
。
(15)函数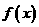 对于任意实数
对于任意实数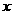 满足条件
满足条件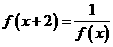 ,若
,若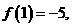 则
则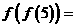 __________。
__________。
解:由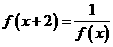 得
得 ,所以
,所以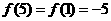 ,则
,则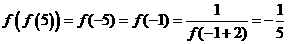 。
。
(16)平行四边形的一个顶点A在平面 内,其余顶点在
内,其余顶点在 的同侧,已知其中有两个顶点到
的同侧,已知其中有两个顶点到 的距离分别为1和2 ,那么剩下的一个顶点到平面
的距离分别为1和2 ,那么剩下的一个顶点到平面 的距离可能是:
的距离可能是:
①1; ②2; ③3; ④4;
以上结论正确的为______________。(写出所有正确结论的编号)
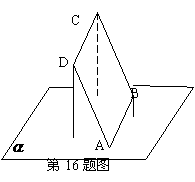 解:如图,B、D到平面
解:如图,B、D到平面 的距离为1、2,则D、B的中点到平面
的距离为1、2,则D、B的中点到平面 的距离为
的距离为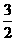 ,所以C到平面
,所以C到平面 的距离为3;
的距离为3;
B、C到平面 的距离为1、2,D到平面
的距离为1、2,D到平面 的距离为
的距离为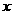 ,则
,则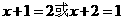 ,即
,即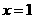 ,所以D到平面
,所以D到平面 的距离为1;
的距离为1;
C、D到平面 的距离为1、2,同理可得B到平面
的距离为1、2,同理可得B到平面 的距离为1;所以选①③。
的距离为1;所以选①③。
(1)设全集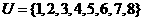 ,集合
,集合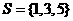 ,
,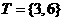 ,则
,则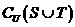 等于( )
等于( )
A.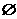 B.
B.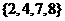 C.
C.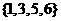 D.
D.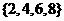
解: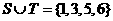 ,则
,则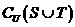 =
=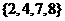 ,故选B
,故选B
(2)不等式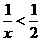 的解集是( )
的解集是( )
A.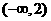 B.
B.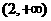 C.
C.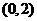 D.
D.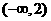
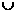
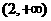
解:由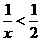 得:
得: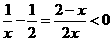 ,即
,即 ,故选D。
,故选D。
(3)函数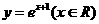 的反函数是( )
的反函数是( )
A. B.
B.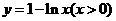
C.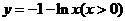 D.
D.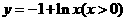
解:由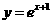 得:
得: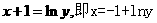 ,所以
,所以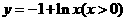 为所求,故选D。
为所求,故选D。
(4)“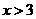 ”是
”是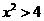 “的( )
“的( )
A.必要不充分条件 B.充分不必要条件
C.充分必要条件 D.既不充分也不必要条件
解:条件集是结论集的子集,所以选B。
(5)若抛物线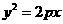 的焦点与椭圆
的焦点与椭圆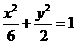 的右焦点重合,则
的右焦点重合,则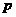 的值为( )
的值为( )
A.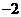 B.
B.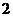 C.
C.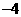 D.
D.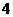
解:椭圆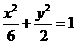 的右焦点为(2,0),所以抛物线
的右焦点为(2,0),所以抛物线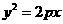 的焦点为(2,0),则
的焦点为(2,0),则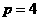 ,故选D。
,故选D。
(6)表面积为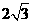 的正八面体的各个顶点都在同一个球面上,则此球的体积为
的正八面体的各个顶点都在同一个球面上,则此球的体积为
A.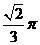 B.
B.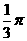 C.
C.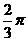 D.
D.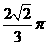
解:此正八面体是每个面的边长均为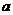 的正三角形,所以由
的正三角形,所以由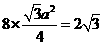 知,
知,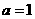 ,则此球的直径为
,则此球的直径为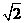 ,故选A。
,故选A。
(7)直线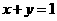 与圆
与圆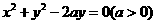 没有公共点,则
没有公共点,则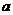 的取值范围是
的取值范围是
A. B.
B.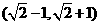 C.
C.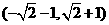 D.
D.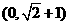
解:由圆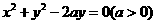 的圆心
的圆心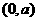 到直线
到直线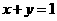 大于
大于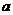 ,且
,且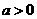 ,选A。
,选A。
(8)对于函数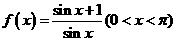 ,下列结论正确的是( )
,下列结论正确的是( )
A.有最大值而无最小值 B.有最小值而无最大值
C.有最大值且有最小值 D.既无最大值又无最小值
解:令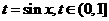 ,则函数
,则函数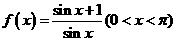 的值域为函数
的值域为函数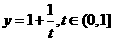 的值域,而
的值域,而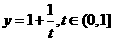 是一个减函减,故选B。
是一个减函减,故选B。
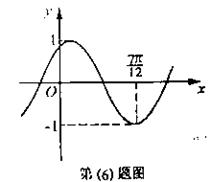 (9)将函数
(9)将函数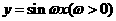 的图象按向量
的图象按向量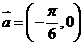 平移,平移后的图象如图所示,则平移后的图象所对应函数的解析式是( )
平移,平移后的图象如图所示,则平移后的图象所对应函数的解析式是( )
A.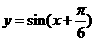 B.
B.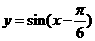
C.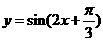 D.
D.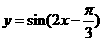
解:将函数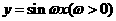 的图象按向量
的图象按向量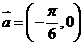 平移,平移后的图象所对应的解析式为
平移,平移后的图象所对应的解析式为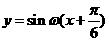 ,由图象知,
,由图象知,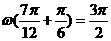 ,所以
,所以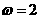 ,因此选C。
,因此选C。
(10)如果实数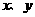 满足条件
满足条件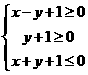 ,那么
,那么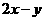 的最大值为( )
的最大值为( )
A.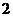 B.
B.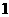 C.
C.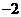 D.
D.
解:当直线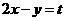 过点(0,-1)时,
过点(0,-1)时,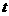 最大,故选B。
最大,故选B。
(11)如果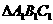 的三个内角的余弦值分别等于
的三个内角的余弦值分别等于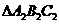 的三个内角的正弦值,则( )
的三个内角的正弦值,则( )
A.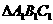 和
和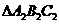 都是锐角三角形 B.
都是锐角三角形 B.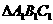 和
和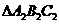 都是钝角三角形
都是钝角三角形
C.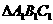 是钝角三角形,
是钝角三角形,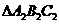 是锐角三角形
是锐角三角形
D.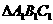 是锐角三角形,
是锐角三角形,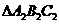 是钝角三角形
是钝角三角形
解: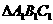 的三个内角的余弦值均大于0,则
的三个内角的余弦值均大于0,则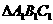 是锐角三角形,若
是锐角三角形,若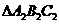 是锐角三角形,由
是锐角三角形,由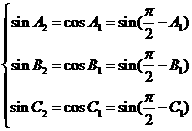 ,得
,得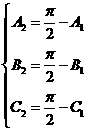 ,那么,
,那么,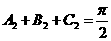 ,所以
,所以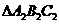 是钝角三角形。故选D。
是钝角三角形。故选D。
(12)在正方体上任选3个顶点连成三角形,则所得的三角形是直角非等腰三角形的概率为( )
A.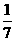 B.
B.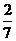 C.
C.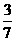 D.
D.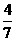
解:在正方体上任选3个顶点连成三角形可得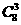 个三角形,要得直角非等腰三角形,则每个顶点上可得三个(即正方体的一边与过此点的一条面对角线),共有24个,得
个三角形,要得直角非等腰三角形,则每个顶点上可得三个(即正方体的一边与过此点的一条面对角线),共有24个,得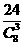 ,所以选C。
,所以选C。
2006年普通高等学校招生全国统一考试(安徽卷)理科数学
第Ⅱ卷(非选择题 共90分)
请用0.5毫米黑色墨水签字笔在答题卡上书写作答,在试题卷上书写作答无效。
15.设F是椭圆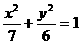 的右焦点,且椭圆上至少有21个不同的点Pi(i=1,2,3,…),使|FP1|,|FP2|,|FP3|,…组成公差为d的等差数列,则d的取值范围为
.
的右焦点,且椭圆上至少有21个不同的点Pi(i=1,2,3,…),使|FP1|,|FP2|,|FP3|,…组成公差为d的等差数列,则d的取值范围为
.
14.若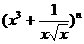 的展开式中的常数项为84,则n=
.
的展开式中的常数项为84,则n=
.
13.同时抛物线两枚相同的均匀硬币,随机变量ξ=1表示结果中有正面向上,ξ=0表示结果中没有正面向上,则Eξ= .
12.已知向量a=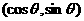 ,向量b=
,向量b=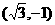 ,则|2a-b|的最大值是
.
,则|2a-b|的最大值是
.
11.设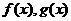 分别是定义在R上的奇函数和偶函数,当
分别是定义在R上的奇函数和偶函数,当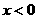 时,
时,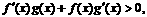
且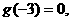 则不等式
则不等式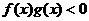 的解集是________________________.
的解集是________________________.
10.从正方体的八个顶点中任取三个点为顶点作三角形,其中直角三角形的个数为( )
A.56 B.52 C.48 D.40
9.设集合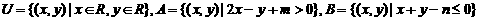 ,那么点P(2,3)
,那么点P(2,3) (
(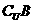 )的充要条件是 ( )
)的充要条件是 ( )
A.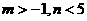 B.
B.
C.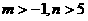 D.
D.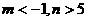
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com