
题目列表(包括答案和解析)
16.连接抛物线上任意四点组成的四边形可能是 (填写所有正确选项的序号).
①菱形 ②有3条边相等的四边形 ③梯形
④平行四边形 ⑤有一组对角相等的四边形
解:①菱形不可能,如果这个四边形是菱形,这时菱形的一条对角线垂直抛物线的对称轴,这时四边形的必有一个顶点在抛物线的对称轴上(非抛物线的顶点); ④平行四边形,也不可能,因为抛物上四个点组成的四边形最多有一组对边平行.故连接抛物线上任意四点组成的四边形可能是②③⑤.
15.某轻轨列车有4节车厢,现有6位乘客准备乘坐,设每一位乘客进入每节车厢是等可能的,则这6位乘客进入各节车厢的人数恰好为0,1,2,3的概率为 .
解:4位乘客进入4节车厢共有256种不同的可能,6位乘客进入各节车厢的人数恰为0,1,2,3的方法共有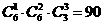 ,∴这6位乘客进入各节车厢的人数恰好为0,1,2,3的概率为
,∴这6位乘客进入各节车厢的人数恰好为0,1,2,3的概率为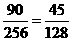 .
.
14.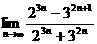 =
.
=
.
解: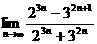 =
=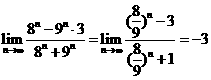
13.已知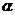 、
、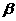 均为锐角,且
均为锐角,且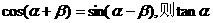 =
.
=
.
解:由已知得1-tanαtanβ=tanα-tanβ,∴tanα=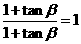 .
.
12.曲线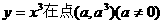 处的切线与x轴、直线
处的切线与x轴、直线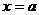 所围成的三角形的面积为
所围成的三角形的面积为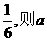 =
.
=
.
解:∵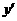 =3x2,∵在(a,a3)处切线为y-a3=3a2(x-a),令y=0,得切线与x轴交点(
=3x2,∵在(a,a3)处切线为y-a3=3a2(x-a),令y=0,得切线与x轴交点( ),切线与直线x=a交于(a,a3),∴曲线
),切线与直线x=a交于(a,a3),∴曲线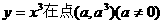 处的切线与x轴、直线
处的切线与x轴、直线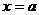 所围成的三角形的面积为S=
所围成的三角形的面积为S=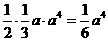 ,令S=
,令S=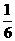 ,解得a=±1.
,解得a=±1.
11.集合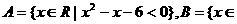 R|
R| 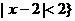 ,则
,则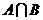 =
.
=
.
解:由题意可知A=(-2,3),B=(0,4),∴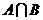 =
=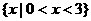 .
.
9.若动点(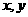 )在曲线
)在曲线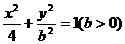 上变化,则
上变化,则 的最大值为 ( )
的最大值为 ( )
A.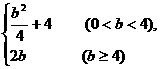 B.
B.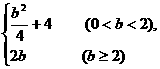
C.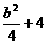 D.2
D.2
解:由题意可设x=2cosα,y=bsinα,则x2+2y=4cos2α+2bsinα=-4sin2α+2bsinα+4
=-2(sin2α-bsinα-2)=-2(sinα-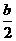 )2+4+
)2+4+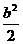 ,∴
,∴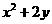 的最大值为
的最大值为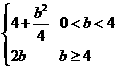 ,选(A)
,选(A)
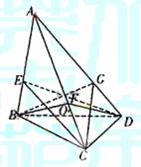 10.如图,在体积为1的三棱锥A-BCD侧棱
10.如图,在体积为1的三棱锥A-BCD侧棱
AB、AC、AD上分别取点E、F、G, 使
AE : EB=AF : FC=AG : GD=2 : 1,记O为
三平面BCG、CDE、DBF的交点,则三棱
锥O-BCD的体积等于 ( )
A.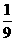 B.
B.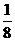
C. 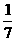 D.
D.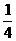

解:如图,BM是平面BCG与平面BDF的交线,CL是平面BCG与平面CDE的交线,则BM子CL的交点即为O.作EG⊥平面BCD,LN⊥平面BCD,OQ⊥平面BCD,设A到平面BCD的高为h,由题意可知
EK=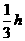 ,LN=
,LN=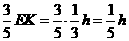 ,∵
,∵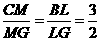 ,∴
,∴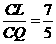
∴OQ=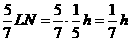 ,∴
,∴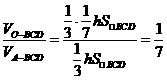 ,选(C)
,选(C)
8.若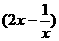 n展开式中含
n展开式中含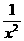 项的系数与含
项的系数与含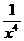 项的系数之比为-5,则n等于 ( )
项的系数之比为-5,则n等于 ( )
A.4 B.6 C.8 D.10
解: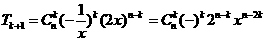 令n-2k=-2,n=2k-2,
令n-2k=-2,n=2k-2,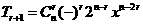 ,令n-2r= -4,n=2r-4由题意得
,令n-2r= -4,n=2r-4由题意得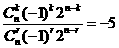 ,
,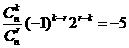 ,∵r-k=1,∴化简得
,∵r-k=1,∴化简得 解得k=4,∴n=6.选(B)
解得k=4,∴n=6.选(B)
7.对于不重合的两个平面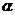 与
与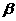 ,给定下列条件:
,给定下列条件:
①存在平面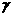 ,使得
,使得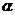 、
、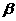 都垂直于
都垂直于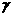 ;
;
②存在平面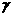 ,使得
,使得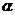 、
、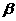 都平行于
都平行于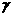 ;
;
③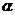 内有不共线的三点到
内有不共线的三点到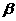 的距离相等;
的距离相等;
④存在异面直线l、m,使得l//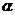 ,l//
,l//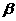 ,m//
,m//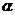 ,m//
,m//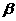 ,
,
其中,可以判定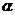 与
与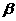 平行的条件有 ( )
平行的条件有 ( )
A.1个 B.2个 C.3个 D.4个
解:命题①③是真命题,选(B)
6.已知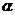 、
、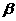 均为锐角,若
均为锐角,若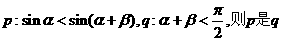 的 ( )
的 ( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
解:∵由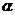 、
、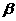 均为锐角,
均为锐角,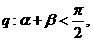 得0<α<α+β<
得0<α<α+β<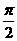 ∴sin(α+β)>sinα,但
∴sin(α+β)>sinα,但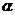 、
、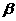 均为锐角,sinα<sin(α+β),不一定能推出α+β<
均为锐角,sinα<sin(α+β),不一定能推出α+β<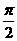 ,如α=
,如α=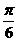 ,β=
,β=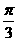 就是一个反例,选(C)
就是一个反例,选(C)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com