
题目列表(包括答案和解析)
12、有两个相同的直三棱柱,高为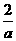 ,底面三角形的三边长分别为
,底面三角形的三边长分别为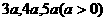 .用它们拼成一个三棱柱或四棱柱,在所有可能的情形中,全面积最小的是一个四棱柱,则
.用它们拼成一个三棱柱或四棱柱,在所有可能的情形中,全面积最小的是一个四棱柱,则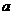 的取值范围是__________.
的取值范围是__________.
见理11
11、函数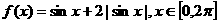 的图象与直线
的图象与直线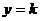 有且仅有两个不同的交点,则
有且仅有两个不同的交点,则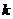 的取值范围是__________.
的取值范围是__________.
见理10
10、在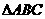 中,若
中,若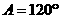 ,AB=5,BC=7,则AC=__________.
,AB=5,BC=7,则AC=__________.
见理9
9、直线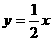 关于直线
关于直线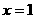 对称的直线方程是__________.
对称的直线方程是__________.
[思路点拨]本题考查一条直线关于已知直线对称的直线方程,可取两个特殊点求出关于直线的对称点的坐标,再由两点式求出直线方程即可.
[正确解答]直线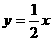 上的点(0,0)关于
上的点(0,0)关于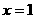 对称的点是(2,0),且所求方程的斜率为-
对称的点是(2,0),且所求方程的斜率为-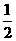 ,因此,直线
,因此,直线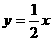 关于直线
关于直线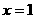 对称的直线方程是:
对称的直线方程是:
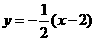 ,整理后得
,整理后得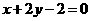 .
.
解法2设所求直线上任意点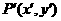 关于直线x=1对称点为
关于直线x=1对称点为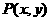 则
则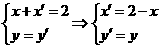 ∵
∵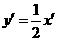 ∴
∴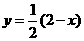 即x+2y-2=0
即x+2y-2=0
[解后反思]解法2是通法,详见理22.
8、某班有50名学生,其中15人选修A课程,另外35人选修B课程.从班级中任选两名学生,他们是选修不同课程的学生的概率是__________.(结果用分数表示)
见理8
7、若椭圆长轴长与短轴长之比为2,它的一个焦点是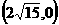 ,则椭圆的标准方程是__________.
,则椭圆的标准方程是__________.
[思路点拨]本题考查椭圆的基础知识,数形的等价转换是解决此类型的关键.
[正确解答]由题意可知,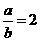 ,
,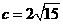 ,又
,又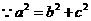 ,解得
,解得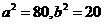 ,
,
所求椭圆的标准方程为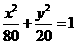 .
.
[解后反思]在求椭圆方程和研究性质时,要深刻理解确定椭圆的形状及大小的主要特征数,如a、b、c、p、e的几何意义及它们的关系式,熟练运用这些公式解决有关问题..
6、若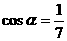 ,
,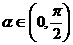 ,则
,则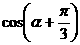 =__________.
=__________.
[思路点拨本题考查两个角和的余弦的求法.熟记公式结构,根据条件求出运用公式必需值,再考虑三角函数的符号.
[正确解答]
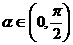 ,
,
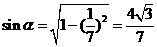 ,
,
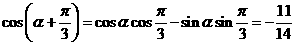 .
.
[解后反思]在三角函数的公式运用过程中取决于满足运用公式的条件,已知三角函数值求同角的其它三角函数值时必须注意符号,否则就无所谓解决三角函数问题.
5、函数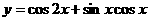 的最小正周期T=__________.
的最小正周期T=__________.
[思路点拨]本题考查二倍角公式等基础知识和变换能力,角的差异(由异角化同角)在同角的条件下,利用三角恒等式化成正弦函数,就可求出最小正周期.
[正确解答]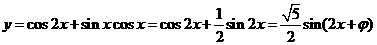 ,得最小正周期为
,得最小正周期为
[解后反思]三角函数的变换要注意变换的方向,消除差异,达到转化.
4、直角坐标平面 中,若定点
中,若定点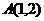 与动点
与动点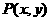 满足
满足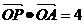 ,则点P的轨迹方程是__________.
,则点P的轨迹方程是__________.
见理3
3、若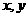 满足条件
满足条件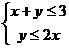 ,则
,则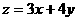 的最大值是__________.
的最大值是__________.
[思路点拨]本题考查线性规划的基础知识,画出可行域,寻求目标函数的最大值.
[正确解答]求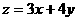 的最大值,即求
的最大值,即求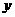 轴上的截距最大值,由图可知,过点(1,2)时有最大值,为11
轴上的截距最大值,由图可知,过点(1,2)时有最大值,为11
[解后反思]线性规划是直线方程的应用,是新增的教学内容.要了解线性不等式表示的平面区域,了解线性规划的定义,会求在线性约束条件下的目标函数的最优解.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com