
题目列表(包括答案和解析)
7.设 ,且
,且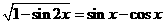 ,则 ( )
,则 ( )
A.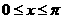 B.
B.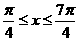 C.
C.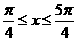 D.
D.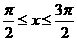
解:∵由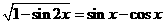 得|sinx-cosx|=sinx-cosx,又
得|sinx-cosx|=sinx-cosx,又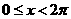 ,
,
∴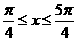 ,选C
,选C
6.若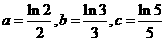 ,则 ( )
,则 ( )
A.a<b<c B.c<b<a C.c<a<b D.b<a<c
解:由题意得a=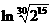 ,b=
,b=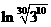 ,c=
,c=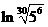 ,
,
∵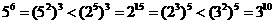 ,∴c<a<b,选C
,∴c<a<b,选C
5.设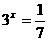 ,则 ( )
,则 ( )
A.-2<x<-1 B.-3<x<-2 C.-1<x<0 D.0<x<1
解: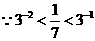 ,
,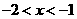 ,选A
,选A
4.设三棱柱ABC-A1B1C1的体积为V,P、Q分别是侧棱AA1、CC1上的点,且PA=QC1,则四棱锥B-APQC的体积为 ( )
A.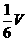 B.
B.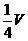 C.
C.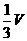 D.
D.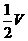
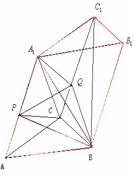 解:如图,
解:如图,
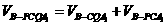 ,∵AF=QC1,
,∵AF=QC1,
∴APQC1,APQC都是平行四边形,
∴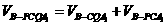 =
=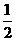 (
(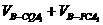 )
)
=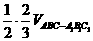 =
=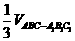 ,选C
,选C
3.在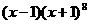 的展开式中
的展开式中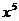 的系数是 ( )
的系数是 ( )
A.-14 B.14 C.-28 D.28
解:(x+1)8展开式中x4,x5的系数分别为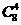 ,
,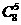 ,∴(x-1)(x+1)8展开式中x5的系数为
,∴(x-1)(x+1)8展开式中x5的系数为
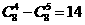 ,选B
,选B
2.已知过点A(-2,m)和B(m,4)的直线与直线2x+y-1=0平行,则m的值为 ( )
A.0 B.-8 C.2 D.10
解:直线2x+y-1=0的一个方向向量为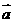 =(1,-2),
=(1,-2),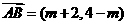 ,由
,由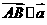
即(m+2)×(-2)-1×(4-m)=0,m=-8,选B
1.已知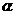 为第三象限角,则
为第三象限角,则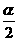 所在的象限是 ( )
所在的象限是 ( )
A.第一或第二象限 B.第二或第三象限
C.第一或第三象限 D.第二或第四象限
解:α第三象限,即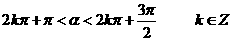 ,
,
∴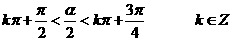 ,可知
,可知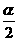 在第二象限或第四象限,选D
在第二象限或第四象限,选D
(17)(本大题满分12分)
设函数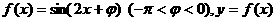 图像的一条对称轴是直线
图像的一条对称轴是直线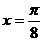 。
。
(Ⅰ)求 ;
;
(Ⅱ)求函数 的单调增区间;
的单调增区间;
(Ⅲ)画出函数 在区间
在区间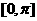 上的图像。
上的图像。
(18)(本大题满分12分)
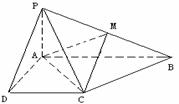
已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,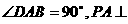 底面ABCD,且PA=AD=DC=
底面ABCD,且PA=AD=DC=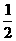 AB=1,M是PB的中点。
AB=1,M是PB的中点。
(Ⅰ)证明:面PAD⊥面PCD;
(Ⅱ)求AC与PB所成的角;
(Ⅲ)求面AMC与面BMC所成二面角的大小。
(19)(本大题满分12分)
已知二次函数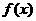 的二次项系数为
的二次项系数为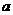 ,且不等式
,且不等式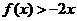 的解集为
的解集为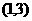 。
。
(Ⅰ)若方程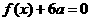 有两个相等的根,求
有两个相等的根,求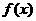 的解析式;
的解析式;
(Ⅱ)若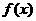 的最大值为正数,求
的最大值为正数,求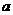 的取值范围。
的取值范围。
(20)(本大题满分12分)
9粒种子分种在甲、乙、丙3个坑内,每坑3粒,每粒种子发芽的概率为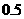 ,若一个坑内至少有1粒种子发芽,则这个坑不需要补种;若一个坑内的种子都没发芽,则这个坑需要补种。
,若一个坑内至少有1粒种子发芽,则这个坑不需要补种;若一个坑内的种子都没发芽,则这个坑需要补种。
(Ⅰ)求甲坑不需要补种的概率;
(Ⅱ)求3个坑中恰有1个坑不需要补种的概率;
(Ⅲ)求有坑需要补种的概率。
(精确到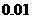 )
)
(21)(本大题满分12分)
设正项等比数列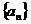 的首项
的首项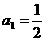 ,前n项和为
,前n项和为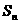 ,且
,且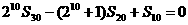 。
。
(Ⅰ)求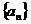 的通项;
的通项;
(Ⅱ)求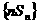 的前n项和
的前n项和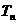 。
。
(22)(本大题满分14分)
已知椭圆的中心为坐标原点O,焦点在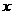 轴上,斜率为1且过椭圆右焦点F的直线交椭圆于A、B两点,
轴上,斜率为1且过椭圆右焦点F的直线交椭圆于A、B两点,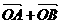 与
与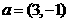 共线。
共线。
(Ⅰ)求椭圆的离心率;
(Ⅱ)设M为椭圆上任意一点,且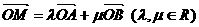 ,证明
,证明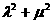 为定值。
为定值。






(13)若正整数m满足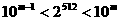 ,则m = 。
,则m = 。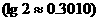
解:∵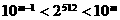 ,∴
,∴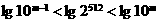 ,即
,即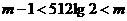 ,
,
∴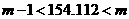 ,即
,即 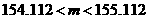 ,∴
,∴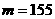 .
.
(14)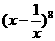 的展开式中,常数项为
。(用数字作答
的展开式中,常数项为
。(用数字作答
解: 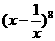 的通项公式为
的通项公式为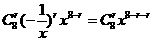 ,令8-2r=0,得r=4,∴常数项为70.
,令8-2r=0,得r=4,∴常数项为70.
(15)从6名男生和4名女生中,选出3名代表,要求至少包含1名女生,则不同的选法共有 种。
解:用剔除法.: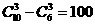 ,∴从6名男生和4名女生中,选出3名代表,要求至少包含1名女生,则不同的选法共有100种。
,∴从6名男生和4名女生中,选出3名代表,要求至少包含1名女生,则不同的选法共有100种。
(16)在正方形 中,过对角线
中,过对角线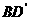 的一个平面交
的一个平面交 于E,交
于E,交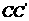 于F,
于F,
①
四边形 一定是平行四边形
一定是平行四边形
②
四边形 有可能是正方形
有可能是正方形
③
四边形 在底面ABCD内的投影一定是正方形
在底面ABCD内的投影一定是正方形
④
四边形 有可能垂直于平面
有可能垂直于平面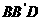
以上结论正确的为 。(写出所有正确结论的编号)
 解:①平面
解:①平面 与相对侧面相交,交线互相平行,
与相对侧面相交,交线互相平行,
∴四边形 一定是平行四边形;
一定是平行四边形;
②四边形 若是正方形,则
若是正方形,则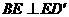 ,又
,又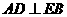 ,
,
∴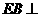 平面
平面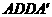 ,产生矛盾;
,产生矛盾;
③四边形 在底面ABCD内的投影是正方形
在底面ABCD内的投影是正方形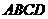 ;
;
④当E、F分别是 、
、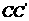 的中点时,
的中点时,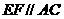 ,又
,又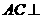 平面
平面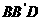 ,
,
∴四边形 有可能垂直于平面,∴填①③④.
有可能垂直于平面,∴填①③④.
(1)设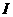 为全集,
为全集,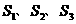 是
是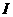 的三个非空子集,且
的三个非空子集,且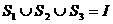 ,则下面论断正确的是
,则下面论断正确的是
(A)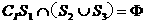 (B)
(B)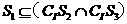
 (C)
(C)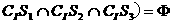 (D)
(D)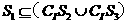
解:∵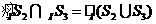 所表示的部分是图中蓝色
所表示的部分是图中蓝色
的部分,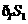 所表示的部分是图中除去
所表示的部分是图中除去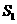 的部分,
的部分,
∴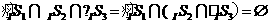 ,故选C.
,故选C.
(2)一个与球心距离为1的平面截球所得的圆面面积为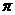 ,则球的表面积为
,则球的表面积为
(A)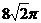 (B)
(B)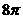 (C)
(C)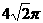 (D)
(D)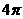
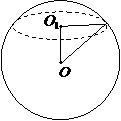 解:∵截面圆面积为
解:∵截面圆面积为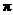 ,∴截面圆半径
,∴截面圆半径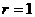 ,
,
∴球的半径为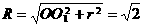 ,
,
∴球的表面积为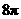 ,故选B.
,故选B.
(3)函数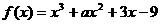 ,已知
,已知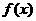 在
在 时取得极值,则
时取得极值,则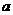 =
=
(A)2 (B)3 (C)4 (D)5
解: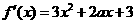 ,令
,令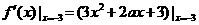 =0,解得a=5,选(D)
=0,解得a=5,选(D)
(4)如图,在多面体ABCDEF中,已知ABCD是边长为1的正方形,且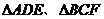 均为正三角形,EF∥AB,EF=2,则该多面体的体积为
均为正三角形,EF∥AB,EF=2,则该多面体的体积为
 (A)
(A)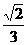 (B)
(B)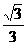
(C)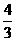 (D)
(D)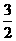
解:如图,过A、B两点分别作AM、BN垂直于EF,垂足分别为M、N,连结DM、CN,可证得DM⊥EF、CN⊥EF,多面体ABCDEF分为三部分,多面体的体积V为
 ,∵
,∵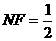 ,
,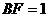 ,∴
,∴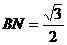 ,
,
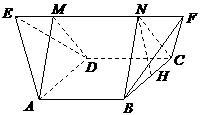 作NH垂直于点H,则H为BC的中点,则
作NH垂直于点H,则H为BC的中点,则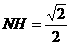 ,∴
,∴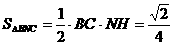 ,∴
,∴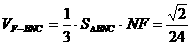 ,
,
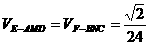 ,
,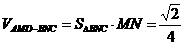 ,∴
,∴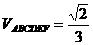 ,故选A.
,故选A.
(5)已知双曲线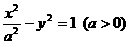 的一条准线为
的一条准线为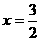 ,则该双曲线的离心率为
,则该双曲线的离心率为
(A)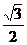 (B)
(B)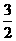 (C)
(C)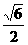 (D)
(D)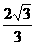
解:由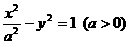 得
得 ,∴
,∴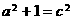 ,抛物线
,抛物线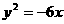 的准线为
的准线为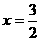 ,因为双曲线
,因为双曲线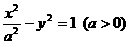 的一条准线与抛物线
的一条准线与抛物线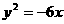 的准线重合,所以
的准线重合,所以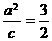 ,解得
,解得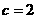 ,所以
,所以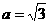 ,所以离心率为
,所以离心率为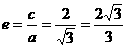 ,故选D.
,故选D.
(6)当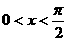 时,函数
时,函数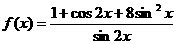 的最小值为
的最小值为
(A)2 (B)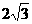 (C)4 (D)
(C)4 (D)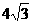
解: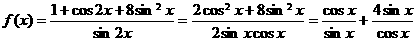
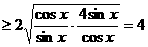 ,当且仅当
,当且仅当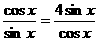 ,即
,即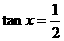 时,取“
时,取“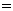 ”,∵
”,∵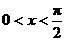 ,∴存在
,∴存在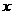 使
使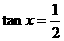 ,这时
,这时 ,故选(C).
,故选(C).
(7)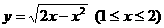 反函数是
反函数是
(A)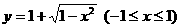
(B)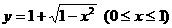
(C)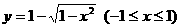
(D)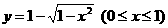
解:由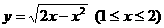 ,得
,得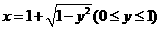 ,故
,故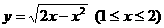 的反函数为
的反函数为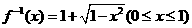 ,选(D)
,选(D)
(8)设 ,函数
,函数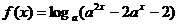 ,则使
,则使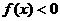 的
的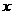 的取值范围是
的取值范围是
(A)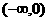 (B)
(B)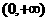 (C)
(C)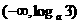 (D)
(D)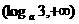
解:∵ ,
,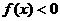 ,∴
,∴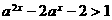 ,解得
,解得 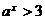 或
或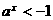 (舍去),
(舍去),
∴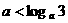 ,故选C.
,故选C.
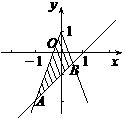
(9)在坐标平面上,不等式组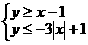 所表示的平面区域的面积为
所表示的平面区域的面积为
(A)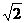 (B)
(B)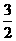 (C)
(C)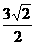 (D)2
(D)2
 解:原不等式化为
解:原不等式化为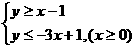 或
或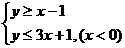 ,
,
所表示的平面区域如右图所示,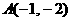 ,
,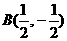 ,
,
∴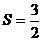 ,故选B
,故选B
(10)在 中,已知
中,已知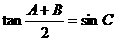 ,给出以下四个论断:
,给出以下四个论断:
①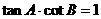 ②
②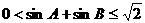
③ ④
④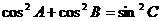
其中正确的是
(A)①③ (B)②④ (C)①④ (D)②③
解:∵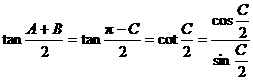 ,
,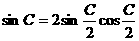 ,
,
∴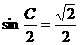 ,∴
,∴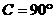 ,
,
∵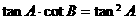 ,∴①不一定成立,
,∴①不一定成立,
∵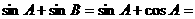
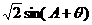 ,∴
,∴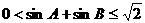 ,∴②成立,
,∴②成立,
∵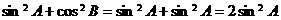 ,∴③不一定成立,
,∴③不一定成立,
∵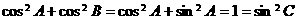 ,∴④成立,故选B.
,∴④成立,故选B.
(11)点O是三角形ABC所在平面内的一点,满足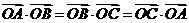 ,则点O是
,则点O是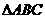 的
的
(A)三个内角的角平分线的交点 (B)三条边的垂直平分线的交点 (C)三条中线的交点 (D)三条高的交点
解: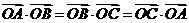 ,即
,即
得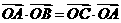 ,
,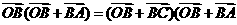
即 ,故
,故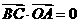 ,
,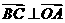 ,同理可证
,同理可证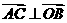 ,∴O是
,∴O是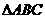 的三条高的交点,选(D)
的三条高的交点,选(D)
(12)设直线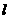 过点
过点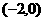 ,且与圆
,且与圆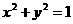 相切,则
相切,则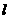 的斜率是
的斜率是
(A)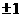 (B)
(B)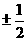 (C)
(C)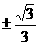 (D)
(D)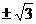
解:设过点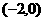 ,且与圆
,且与圆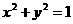 相切的直线
相切的直线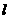 的斜率为k,则直线
的斜率为k,则直线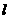 的方程为:y-kx+2k=0,k满足:1=
的方程为:y-kx+2k=0,k满足:1=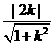 得k=
得k=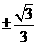 ,选(D).
,选(D).
第Ⅱ卷
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com