
题目列表(包括答案和解析)
13.对于函数 定义域中任意的
定义域中任意的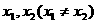 ,有如下结论:
,有如下结论:
①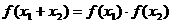 ; ②
; ②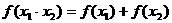 ;
;
③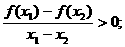 ④
④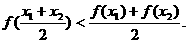
当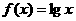 时,上述结论中正确结论的序号是
.
时,上述结论中正确结论的序号是
.
[答案]②③
[详解]
对于①②可以用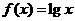
直接验证即可②满足题意
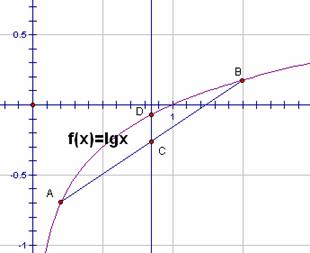
对于③④如右图所示:
对于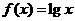 图象上任意不同
图象上任意不同
两点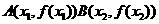
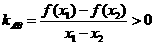 显然成立(可以用
显然成立(可以用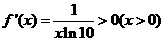 )故③正确
)故③正确
再有AB中点C(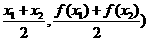 过C作
过C作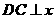 轴交
轴交 于D(
于D(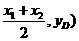
D在 上有:
上有: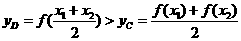 故④不正确
故④不正确
[名师指津]
本题主要考查了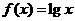 函数运算性质以及直线斜率应用,题目较综合.
函数运算性质以及直线斜率应用,题目较综合.
12.过原点作曲线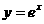 的切线,则切点的坐标为
,切线的斜率为 .
的切线,则切点的坐标为
,切线的斜率为 .
 [答案]
[答案]
[详解]
(略)
[名师指津]
(略)
11.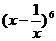 的展开式中的常数项是
. (用数字作答)
的展开式中的常数项是
. (用数字作答)
[答案]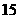
[详解]
对于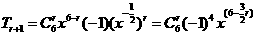 当
当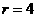 时第5项为常数项,即
时第5项为常数项,即
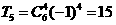 .
.
[名师指津]
二项式定理第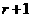 项的通项公式
项的通项公式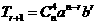 的运用在往年高考中经常遇到.
的运用在往年高考中经常遇到.
10.已知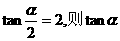 的值为
,
的值为
,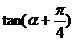 的值为
.
的值为
.
[答案]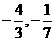
[详解]
(I)因为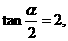
所以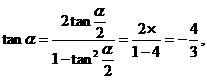
所以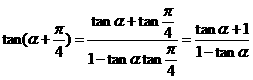
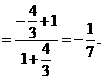
[名师指津]
本题还考查了倍角的正切公式与两角和的正公式.三角函数知识的考查每年题目难度都不是很
大,应该抓基本公式与基本题型的解决.
9.若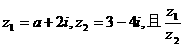 为纯虚数,则实数a的值为
.
为纯虚数,则实数a的值为
.
[答案]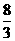
[详解]

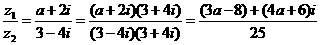 为纯虚数
为纯虚数
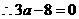 且
且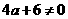
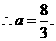
[名师指津]
复数的四则运算,复数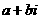 为实数、纯虚数的充要条件,复数的模作为复数内容的重点.
为实数、纯虚数的充要条件,复数的模作为复数内容的重点.
8.函数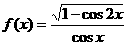 ( )
( )
A.在 上递减
上递减
B.在 上递减
上递减
C.在 上递减
上递减
D.在 上递减
上递减
[答案]A
[详解]
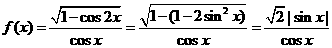
当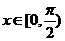 或
或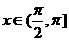 时
时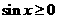
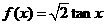 在
在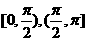 上为增函数
上为增函数
当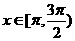 或
或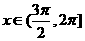 时
时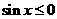
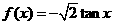 在
在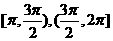 上为减函
上为减函
数.
[名师指津]
对二倍角余弦公式及两个变式的的正用逆用应熟练,对处理绝对值问题的基本思路是用分类
讨论的思想去掉绝对值然后再研究问题,正切函数的单调区间.
第Ⅱ卷(共110分)
7.北京《财富》全球论坛期间,某高校有14名志愿者参加接待工作,若每天早、中、晚三班,每4人,每人每天最多值一班,则开幕式当天不同的排班种数为 ( )
A.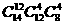 B.
B.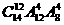 C.
C.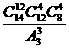 D.
D.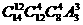
[答案]A
[详解]
本题可以先从14人中选出12人即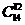 ,然后从这12人中再选出4人做为早班即
,然后从这12人中再选出4人做为早班即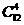 ,最后再从剩
,最后再从剩
余的8人选出4人安排为中班即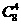 ,剩下的4个安排为晚班,以上为分步事件应用乘法原理可得
,剩下的4个安排为晚班,以上为分步事件应用乘法原理可得
不同的排法为: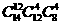 .
.
[名师指津]
排列组合中的分步计数原理与分类计数原理做为解决此类问题的基础.
6.在正四面体P-ABC中,D,E,F分别是AB,BC,CA的中点,下面四个结论中不成立的是 ( )
A.BC//平面PDF B.DF⊥PAE
C.平面PDF⊥平面ABC D.平面PAE⊥平面ABC
[答案]C
[详解]
如图所示:DF∥BC可得A正确
 可得
可得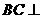 平面
平面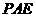
从而得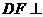 平面
平面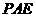 B正确
B正确
 平面ABC 则平面
平面ABC 则平面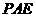
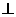 平面ABC D正确
平面ABC D正确
[名师指津]
立体几何中的几个重要模型正四面体、正三棱锥、正四棱等中的边边、边面、面面
之间的关系为这一章节的重点内容,高考题的大部分题目都以它们为背景.
5.对任意的锐角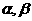 ,下列不等关系中正确的是 ( )
,下列不等关系中正确的是 ( )
A.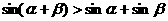 B.
B.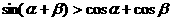
C.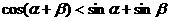 D.
D.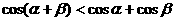
[答案]D
[详解]
当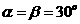 时可排除A、B选项,当
时可排除A、B选项,当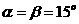 时代入C选项中,即:
时代入C选项中,即: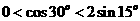
两边平方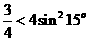
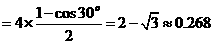 矛盾故选D
矛盾故选D
[名师指津]
特殊值反代入的解题思想在高考选择题的解决过程中经常用到.本题只是简单的两组特殊角代
入即可解决问题.特殊值解选择题关键是恰到好处地选取特殊值如:数值类经常考虑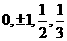
角类的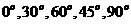 真数类
真数类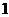 ,底的
,底的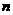 次幂或是
次幂或是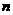 次幂的倒数等等
次幂的倒数等等
4.从原点向圆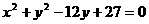 作两条切线,则该圆夹在两条切线间的劣弧长为( )
作两条切线,则该圆夹在两条切线间的劣弧长为( )
A.π B.2π C.4π D.6π
[答案]B
[详解]
将圆的方程配方得: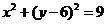 圆心在
圆心在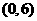 半径为3,如图:
半径为3,如图:
在图中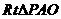 中,
中,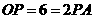 ,从而得到
,从而得到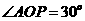 ,
,
即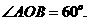 可求
可求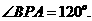
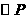 的周长为
的周长为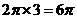
劣弧长为周长的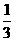 ,可求得劣弧长为
,可求得劣弧长为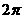 .
.
[名师指津]
以数形结合的思想解决此类题,抓图中直角三角形中边角关系.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com