
题目列表(包括答案和解析)
( 1 ) 若集合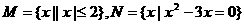 ,则M∩N
,则M∩N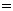 ( )
( )
A.{3} B.{0} C.{0,2} D.{0,3}
[答案]B
解: ∵由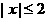 ,得
,得 ,
,
由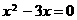 ,得
,得 ,
,
∴M∩N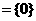 ,故选B.
,故选B.
( 2 ) 若 ,其中a、b∈R,i是虚数单位,则
,其中a、b∈R,i是虚数单位,则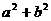 = ( )
= ( )
A.0 B.2 C.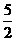 D.5
D.5
[答案]D
解: ∵  ,∴
,∴ ,
,
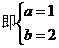 ,
,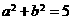 ,故选D.
,故选D.
( 3 ) 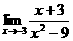 = ( )
= ( )
A.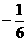 B.0 C.
B.0 C. D.
D.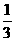
[答案]A
解: 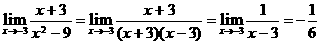 ,故选A.
,故选A.
 ( 4 ) 已知高为3的直棱锥
( 4 ) 已知高为3的直棱锥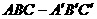 的底面是边长为1的正三角形
的底面是边长为1的正三角形
(如图1所示),则三棱锥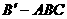 的体积为
( )
的体积为
( )
A. B.
B.
C.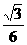 D.
D.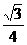
[答案]D
解:∵ 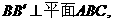
∴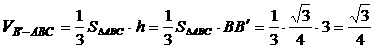 .
.
故选D.
( 5 ) 若焦点在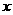 轴上的椭圆
轴上的椭圆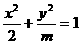 的离心率为
的离心率为 ,则m=( )
,则m=( )
A.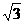 B.
B.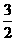 C.
C.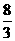 D.
D.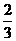
[答案]B
解: ∵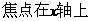 ,∴
,∴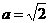 ,
,
∵
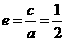 ,∴
,∴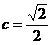 ,
,
∴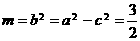 ,故选B.
,故选B.
( 6 )函数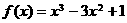 是减函数的区间为 ( )
是减函数的区间为 ( )
A.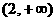 B.
B. C.
C. D.(0,2)
D.(0,2)
[答案]D
解: ∵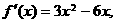
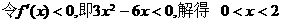 ,故选D.
,故选D.
( 7 ) 给出下列关于互不相同的直线 、
、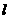 、
、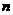 和平面
和平面 、
、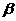 ,的四个命题:
,的四个命题:
①若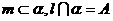 ,点
,点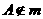 ,则
,则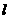 与
与 不共面;
不共面;
②若m、l是异面直线,  , 且
, 且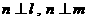 ,则
,则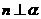 ;
;
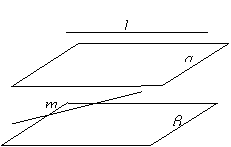
③若 ,
, 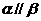 ,则
,则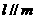 ;
;
 ④若
④若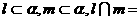 点
点 ,
,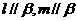 ,则
,则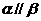 .
.
其中为假命题的是
A.① B.② C.③ D.④
[答案]C
解:③是假命题,如右图所示
满足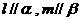 ,
, 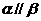 ,
,
但 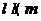 ,故选C.
,故选C.
( 8 ) 先后抛掷两枚均匀的正方体骰子(它们的六个面分别标有点数1、2、3、4、5、6),骰子
朝上的面的点数分别为X、Y,则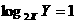 的概率为 ( )
的概率为 ( )
A. B.
B.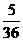 C.
C.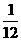 D.
D.
[答案]C
解:满足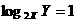 的X、Y有(1, 2),(2, 4),(3, 6)这3种情况,而总的可能数有36种,所以
的X、Y有(1, 2),(2, 4),(3, 6)这3种情况,而总的可能数有36种,所以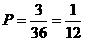 ,故选C.
,故选C.
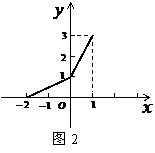
( 9 ) 在同一平面直角坐标系中,函数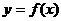 和
和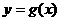 的图像
的图像
关于直线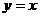 对称.现将
对称.现将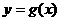 图像沿x轴向左平移2个单位,
图像沿x轴向左平移2个单位,
再沿y轴向上平移1个单位,所得的图像是由两条线段组成的折线
(如图2所示),则函数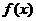 的表达式为
的表达式为
A.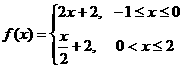 B.
B.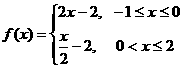
C.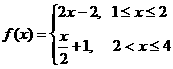 D.
D.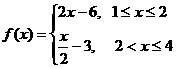
[答案]A
解:将图象沿y轴向下平移1个单位,再沿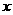 轴向右平移2个单位得下图A,从而可以得到
轴向右平移2个单位得下图A,从而可以得到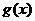 的图象,故
的图象,故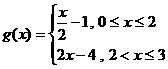 ,
,
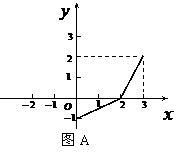 ∵函数
∵函数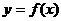 和
和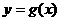 的图像关于直线
的图像关于直线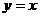 对称,
对称,
∴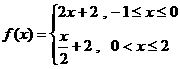 ,故选A.
,故选A.
(也可以用特殊点检验获得答案)
(10)已知数列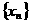 满足
满足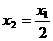 ,
,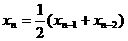 ,
,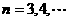 .若
.若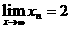 ,则
,则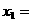
A.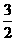 B.3 C.4 D.5
B.3 C.4 D.5
[答案]B
解法一:特殊值法,当 时,
时,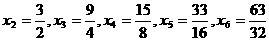
由此可推测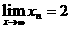 ,故选B.
,故选B.
解法二:∵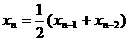 ,∴
,∴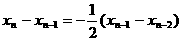 ,
,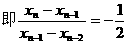 ,
,
∴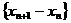 是以(
是以(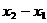 )为首项,以
)为首项,以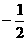 为公比6的等比数列,
为公比6的等比数列,
令 ,则
,则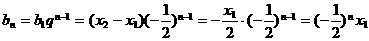
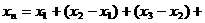 …
…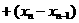
 …
…
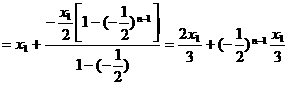
∴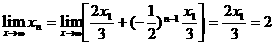 ,∴
,∴ ,故选B.
,故选B.
解法三:∵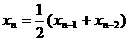 ,∴
,∴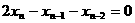 ,
,
∴其特征方程为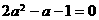 ,
,
解得 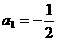 ,
,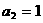 ,
,
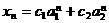 ,
,
∵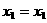 ,
,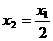 ,∴
,∴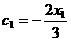 ,
,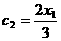 ,
,
∴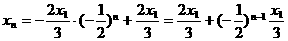 ,以下同解法二.
,以下同解法二.
22.(本小题满分14分)
已知方向向量为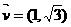 的直线l过点(
的直线l过点(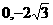 )和椭圆
)和椭圆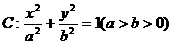 的焦点,且椭圆C的中心关于直线l的对称点在椭圆C的右准线上.
的焦点,且椭圆C的中心关于直线l的对称点在椭圆C的右准线上.
(Ⅰ)求椭圆C的方程;
(Ⅱ)是否存在过点E(-2,0)的直线m交椭圆C于点M、N,满足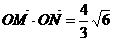 cot
cot
∠MON≠0(O为原点).若存在,求直线m的方程;若不存在,请说明理由.
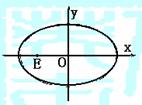
解:(Ⅰ)由题意可得直线ι: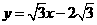 ,
①
,
①
过原点垂直ι的方程为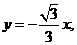 ②
②
解①②得x=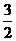 .∵椭圆中心O(0,0)关于直线ι的对称点在椭圆C的右准线上,
.∵椭圆中心O(0,0)关于直线ι的对称点在椭圆C的右准线上,
∴ .∵直线ι过椭圆焦点,∴该焦点坐标为(2,0).
.∵直线ι过椭圆焦点,∴该焦点坐标为(2,0).
∴a2=6,c=2,b2=2,故椭圆C的方程为 . ③
. ③
(Ⅱ)设M(x1,y1),N(x2,y2),当直线m不垂直x轴时,直线m:y=k(x+2)代入③,整理得
(3k2+1)x2+12k2x+12k2-6=0,则x1+x2= ,x1x2=
,x1x2= ,
,
|MN|=
点O到直线MN的距离d=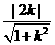 .∵
.∵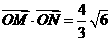 cot∠MON,即
cot∠MON,即
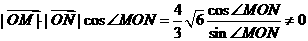 ,
,
∴ ,∴
,∴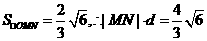 ,
,
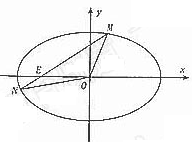
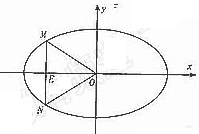 即
即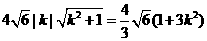 .整理得
.整理得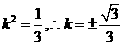 .
.
当直线m垂直x轴时,也满足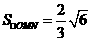
故直线m的方程为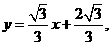 或y=
或y=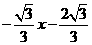 或x=-2.
或x=-2.
经检验上述直线均满足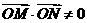 .
.
所在所求直线方程为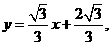 或y=
或y=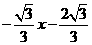 或x=-2..
或x=-2..
21.(本小题满分12分)
如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
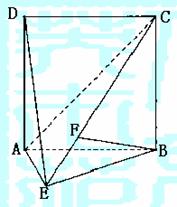 (Ⅰ)求证AE⊥平面BCE;
(Ⅰ)求证AE⊥平面BCE;
(Ⅱ)求二面角B-AC-E的大小;
(Ⅲ)求点D到平面ACE的距离.

解法一:(Ⅰ) ∵BF⊥平面ACE,∴BF⊥AE,∵二面角D-AB-E为直二面角,且CB⊥AB,
∴CB⊥平面ABE,∴CB⊥AE,∴AE⊥平面BCE
(Ⅱ)连结BD交AC于G,连结FG,∵正方形ABCD边长为2,∴BG⊥AC,BG= ,
,
∵BF⊥平面ACE,由三垂线定理的逆定理得FG⊥AC,∴∠BCF是二面角B-AC-E的平面角,
由(Ⅰ)AE⊥平面BCE,∴AE⊥EB.又∵AE=EB,∴在等腰直角三角形中,BE= .
.
又∵直角三角形BCE中,EC=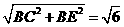 ,BF=
,BF=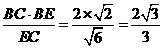
∴直角三角形BFG中,sin∠BGF= ,∴二面角B-AC-E等于arcsin
,∴二面角B-AC-E等于arcsin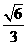 .
.
,(Ⅲ)过E作EO⊥AB交AB于O,OE=1,∵二面角D-AB-E为直二面角,∴EO⊥平面ABCD.
设D到平面ACE的距离为h,∵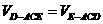 ,∴
,∴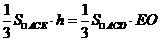 .
.
∵AE⊥平面BCE,∴AE⊥EC.∴h=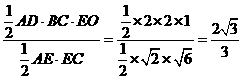 .
.
∴点D点D到平面ACE的距离为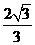 .
.
解法二:(Ⅰ)同解法一.
(Ⅱ)以线段AB的中点为原点O,OE所在直线为x轴,AB所在直线为y轴,过O点平行于AD的直线为z轴,建立空间直角坐标系O-xyz,如图
∵AE⊥平面BCE,BE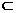 面BCE,∴AE⊥BE,在直角三角形AEB中,AB=2,O为AB的中点
面BCE,∴AE⊥BE,在直角三角形AEB中,AB=2,O为AB的中点
∴OE=1,A(0,-1,0),E(1,0,0),C(0,1,2),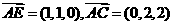
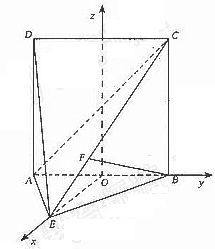
设平面AEC的一个法向量 =(x,y,z),则
=(x,y,z),则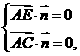 即
即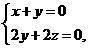 解得
解得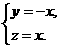
令x=1,得 =(1,-1,1)是平面EAC的一个法向量,又平面BAC的一个法向量为
=(1,-1,1)是平面EAC的一个法向量,又平面BAC的一个法向量为 =(1,0,0),
=(1,0,0),
∴cos(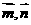 )=
)=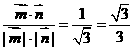
∴二面角B-AC-E的大小为arccos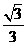 .
.
(Ⅲ)∵AD∥z轴,AD=2,∴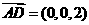 ,∴点D到平面ACE的距离
,∴点D到平面ACE的距离
d=| |
|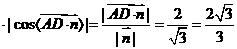 .
.
20.(本小题满分12分)
已知函数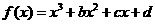 的图象过点P(0,2),且在点M(-1,f(-1))处的切线方程为
的图象过点P(0,2),且在点M(-1,f(-1))处的切线方程为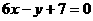 .
.
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)求函数 的单调区间.
的单调区间.
解:(Ⅰ)由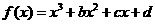 的图象过点P(0,2),d=2知,所以
的图象过点P(0,2),d=2知,所以 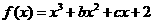 ,
,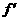 (x)=3x2+2bx+c,由在(-1,(-1))处的切线方程是6x-y+7=0,知
(x)=3x2+2bx+c,由在(-1,(-1))处的切线方程是6x-y+7=0,知
-6-f(-1)+7=0,即f(-1)=1, 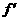 (-1)=6,∴
(-1)=6,∴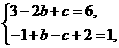 即
即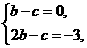 解得b=c=-3.
解得b=c=-3.
故所求的解析式为f(x)=x3-3x-3+2,
(Ⅱ) 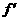 (x)=3x2-6x-3,令3x2-6x-3=0即x2-2x-1=0,解得x1=1-
(x)=3x2-6x-3,令3x2-6x-3=0即x2-2x-1=0,解得x1=1- ,x2=1+
,x2=1+ ,
,
当x<1- 或x>1+
或x>1+ 时,
时, 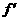 (x)>0;当1-
(x)>0;当1- <x<1+
<x<1+ 时,
时, 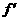 (x)<0
(x)<0
∴f(x)=x3-3x2-3x+2在(1+ ,+∞)内是增函数,在(-∞, 1-
,+∞)内是增函数,在(-∞, 1- )内是增函数,在(1-
)内是增函数,在(1- ,1+
,1+ )内是减函数.
)内是减函数.
19.(本小题满分12分)
已知{ }是公比为q的等比数列,且
}是公比为q的等比数列,且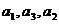 成等差数列.
成等差数列.
(Ⅰ)求q的值;
(Ⅱ)设{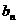 }是以2为首项,q为公差的等差数列,其前n项和为Sn,当n≥2时,比较Sn与bn的大小,并说明理由.
}是以2为首项,q为公差的等差数列,其前n项和为Sn,当n≥2时,比较Sn与bn的大小,并说明理由.
解:(Ⅰ)由题意得:2a2=a1+a2,即2a2q2=a1+a1q,,∵a1≠0,∴2q2-q-1=0,∴q=1或q=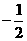
(Ⅱ)若q=1,则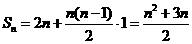 .
.
当n≥2时,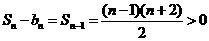 ,故
,故
若q=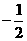 ,则
,则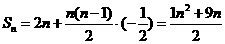 ,
,
当n≥2时, 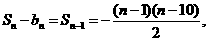 ,
,
故对于n∈N+,当2≤n≤9时,Sn>bn;当n=10时, Sn=bn;当n≥11时, Sn<bn
18.(本小题满分12分)
甲、乙两人在罚球线投球命中的概率分别为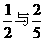 .
.
(Ⅰ)甲、乙两人在罚球线各投球一次,求恰好命中一次的概率;
(Ⅱ)甲、乙两人在罚球线各投球二次,求这四次投球中至少一次命中的概率.
(Ⅰ)依题意,记“甲投一次命中”为事件A,“乙投一次命中”为事件B,则P(A)=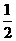 ,P(B)=
,P(B)=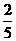 ,P(
,P( )=
)=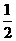 ,P(
,P(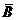 )=
)=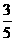
甲、乙两人在罚球线各投球一次,求恰好命中一次的事件为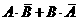
P(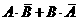 )=P(
)=P(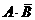 )+P(
)+P(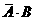 )=
)=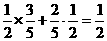
答:甲、乙两人在罚球线各投球一次,求恰好命中一次的概率为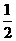
(Ⅱ)∵事件“甲、乙两人在罚球线各投球二次不命中” 的概率是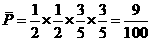
∴甲、乙两人在罚球线各投球二次,至少有一次命中的概率为P=1-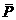 =1-
=1-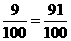
答:甲、乙两人在罚球线各投球二次,至少有一次命中的概率为
17.(本小题满分12分)
已知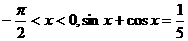 .
.
(Ⅰ)求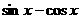 的值;
的值;
(Ⅱ)求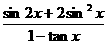 的值.
的值.
解:(Ⅰ)由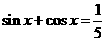 ,得
,得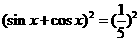 ,得2sinxcosx=
,得2sinxcosx= ,∵(sinx-cosxx)2=1-2sinxcosx=
,∵(sinx-cosxx)2=1-2sinxcosx=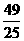 ,又
,又 ∴sinx<0cosx>0,∴sinx-cosx=-
∴sinx<0cosx>0,∴sinx-cosx=-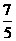
(Ⅱ) 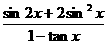 =
=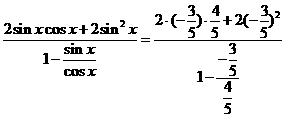 =
=
16.把下面不完整的命题补充完整,并使之成为真命题.
若函数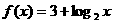 的图象与
的图象与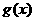 的图象关于
对称,则函数
的图象关于
对称,则函数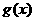 =
=
.
(注:填上你认为可以成为真命题的一种情形即可,不必考虑所有可能的情形)
解:若函数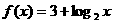 的图象与
的图象与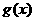 的图象关于y=x对称, 则函数
的图象关于y=x对称, 则函数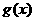 =2x-3.
=2x-3.
15.非负实数x、y满足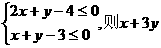 的最大值为
.
的最大值为
.
解: 如右图,在同一平面直角坐标系中画出下列
如右图,在同一平面直角坐标系中画出下列
曲线方程的图象:
2x+y-4=0 (x≥0,y≥0)
x+y-3=0 (x≥0,y≥0)
它们分别是线段AB,CD
则非负实数x、y满足的不等式组
 表示的区域为DMAO,
表示的区域为DMAO,
令x+3y=b,使直线系x+3y=b通过区域DMAO且使b为取得最大值,当且仅当直线x+3y=b过点D(0,3)这时最大值b=9.
14.在△ABC中,∠A=90°,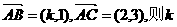 的值是
.
的值是
.
解:由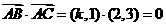 ,得k=
,得k=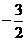
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com