
题目列表(包括答案和解析)
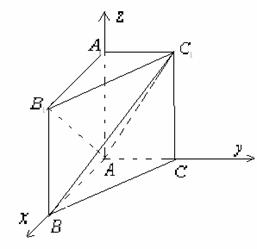
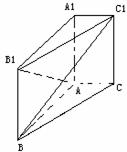
19、[理]在直棱柱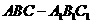 中,已知
中,已知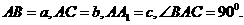
(1)求使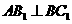 的充要条件(用
的充要条件(用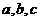 表示);
表示);
(2)求证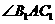 为锐角;
为锐角;
(3)若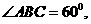 则
则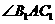 是否可能为
是否可能为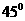 ?证明你的结论.
?证明你的结论.
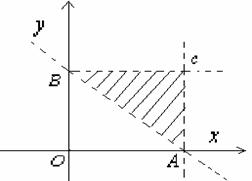
[文]设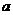 为正数,直角坐标平面内的点集
为正数,直角坐标平面内的点集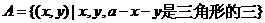
(1)画出A所表示的平面区域;
(2)在平面直角坐标系中,规定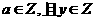 时,
时,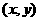 称为格点,当
称为格点,当 时,A内有几个格点(本小题只要直接写出结果即可);
时,A内有几个格点(本小题只要直接写出结果即可);
 (3)点集A连同它的边界构成的区域记为
(3)点集A连同它的边界构成的区域记为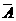 ,若圆
,若圆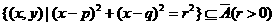 ,求
,求 的最大值.
的最大值.
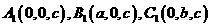 ------2分
------2分
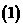
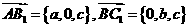
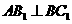
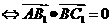
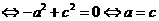
即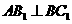 的充分条件是
的充分条件是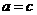 ---------------------------------------------6分
---------------------------------------------6分

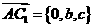 ,
,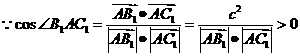
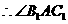 为锐角-------------------------------------------------------------------8分
为锐角-------------------------------------------------------------------8分
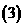
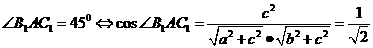
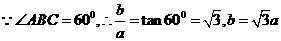
代入上式得,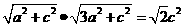
解得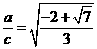 ---------------------------------------------------------------11分
---------------------------------------------------------------11分
 若
若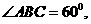 解当
解当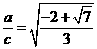 时,
时,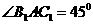 --------------14分
--------------14分
[文] 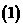
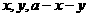 是三角形三边长
是三角形三边长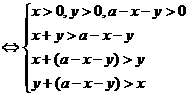
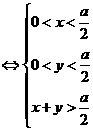 ---------------------------------------8分
---------------------------------------8分
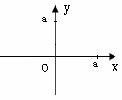
 点集
点集 构成的平面区域为等腰直角三角形
构成的平面区域为等腰直角三角形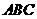 ,如上图阴影部分表示(不包括边界)。
,如上图阴影部分表示(不包括边界)。
 当
当 时,
时, 内有3个格点--------------------------------------------------------10分
内有3个格点--------------------------------------------------------10分
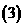
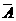 为包括边界的三角形区域,形内的最大圆即是
为包括边界的三角形区域,形内的最大圆即是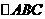 的内切圆,其半径为
的内切圆,其半径为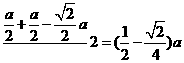

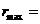
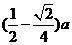 -------------------------------------------------------------------------14分
-------------------------------------------------------------------------14分
18、已知数列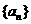 的通项公式为
的通项公式为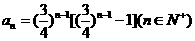 .求
.求
(1)求数列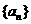 中的最大项及其值;
中的最大项及其值;
(2)求数列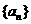 中的最小项及其值.
中的最小项及其值.
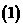 当
当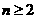 时,
时,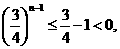 从而
从而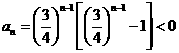
故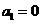 为数列
为数列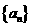 的最大项----------------------------------------------------------------------4分
的最大项----------------------------------------------------------------------4分

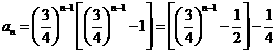
 随
随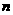 的增大而减小,又
的增大而减小,又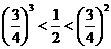 --------------------------------------------8分
--------------------------------------------8分
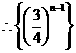 中与
中与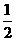 距离最近的数是
距离最近的数是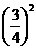
故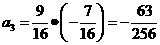 是数列
是数列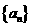 的最小项--------------------12分
的最小项--------------------12分
17、已知向量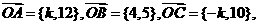 且A、B、C三点共线,求
且A、B、C三点共线,求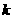 的值.
的值.
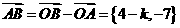 ,
,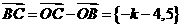 ----------------------------4分
----------------------------4分
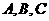 三点共线,
三点共线, 存在实常数
存在实常数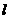 ,使
,使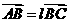 -----------------------------------------8分
-----------------------------------------8分
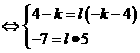
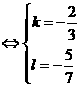
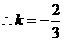 -----------------------------------------------------------------------------------------------12分
-----------------------------------------------------------------------------------------------12分
16、设b>0,二次函数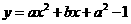 的图像为下列之一,
的图像为下列之一,

则a的值为 ( B )
A. 1
B. 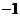 C.
C.
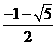 D.
D.
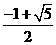
15、已知两线段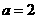 ,b=
,b=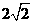 ,若以a,b为边作三角形,则a边所对的角A的取值范围为(D )
,若以a,b为边作三角形,则a边所对的角A的取值范围为(D )
A.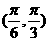 B .
B .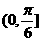 C.
C. 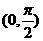 D.
D.
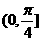
14、“a=b”直线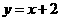 与圆
与圆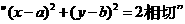 的
(
A )
的
(
A )
A. 充分不必要条件, B .必要不充分条件
C. 充要条件 D. 既不充分又不必要条件
13、已知函数f(x)= 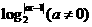 满足
满足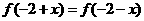 ,则实数a的值为 ( B )
,则实数a的值为 ( B )
A. 1
B. 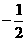 C.
C.  D.
-1
D.
-1
14、 已知集合A= 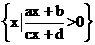 ,这里a,b,c,d为实数,若
,这里a,b,c,d为实数,若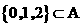 ,且
,且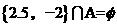 ,则函数
,则函数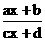 可以是
可以是 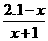 (只有写出一个满足条件的函数).
(只有写出一个满足条件的函数).
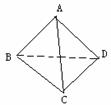
11、已知四面体ABCD,沿棱AB、AC、AD剪开,铺成平面图形,
得到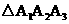 (如图),试写出四面体ABCD应满足的一个性质:
(如图),试写出四面体ABCD应满足的一个性质:
四面体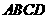 的每组对棱相等(答案不唯一,可填“四面体
的每组对棱相等(答案不唯一,可填“四面体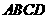 的四个面是四个全等三角形”;或填“四面体每个顶点为公共顶点的三个面角之和为
的四个面是四个全等三角形”;或填“四面体每个顶点为公共顶点的三个面角之和为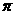 ”) .
”) .
11、 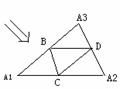
 已知双曲线
已知双曲线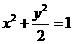 的焦点为
的焦点为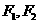 ,点M在双曲线上,且
,点M在双曲线上,且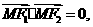 则点M到x轴的距离为
则点M到x轴的距离为 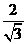 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com