
题目列表(包括答案和解析)
40.(陕西卷)某校从8名教师中选派4名教师同时去4个边远地区支教(每地1人),其中甲和乙不同去,则不同的选派方案共有 种 .
解析:可以分情况讨论,① 甲去,则乙不去,有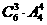 =480种选法;②甲不去,乙去,有
=480种选法;②甲不去,乙去,有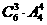 =480种选法;③甲、乙都不去,有
=480种选法;③甲、乙都不去,有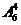 =360种选法;共有1320种不同的选派方案.
=360种选法;共有1320种不同的选派方案.
39.(陕西卷) (2x-)6展开式中常数项为 (用数字作答)
解析:(2x-)6展开式中常数项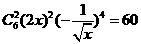 .
.
38.(陕西卷)某校从8名教师中选派4名教师同时去4个边远地区支教(每地1人),其中甲和乙不同去,甲和丙只能同去或同不去,则不同的选派方案共有 种
解析:某校从8名教师中选派4名教师同时去4个边远地区支教(每地1人),其中甲和乙不同去,甲和丙只能同去或同不去,可以分情况讨论,① 甲、丙同去,则乙不去,有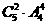 =240种选法;②甲、丙同不去,乙去,有
=240种选法;②甲、丙同不去,乙去,有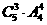 =240种选法;③甲、乙、丙都不去,有
=240种选法;③甲、乙、丙都不去,有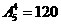 种选法,共有600种不同的选派方案.
种选法,共有600种不同的选派方案.
37.(陕西卷) (3x-)12展开式x-3的系数为 (用数字作答)
解析:(3x-)12展开式中,x-3项为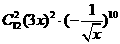 =594
=594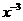 ,
,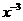 的系数是594.
的系数是594.
35.(全国卷I)安排7位工作人员在5月1日到5月7日值班,每人值班一天,其中甲、乙二人都不能安排在5月1日和2日,不同的安排方法共有__________种。(用数字作答)解析:先安排甲、乙两人在后5天值班,有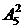 =20种排法,其余5人再进行排列,有
=20种排法,其余5人再进行排列,有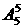 =120种排法,所以共有20×120=2400种安排方法。
=120种排法,所以共有20×120=2400种安排方法。
36(全国II)在(x4+)10的展开式中常数项是 (用数字作答)
解析: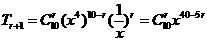 要求常数项,即40-5r=0,可得r=8代入通项公式可得
要求常数项,即40-5r=0,可得r=8代入通项公式可得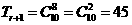
34.(辽宁卷)5名乒乓球队员中,有2名老队员和3名新队员.现从中选出3名队员排成1、2、3号参加团体比赛,则入选的3名队员中至少有一名老队员,且1、2号中至少有1名新队员的排法有_______种.(以数作答)
[解析]两老一新时, 有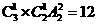 种排法;
种排法;
两新一老时, 有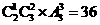 种排法,即共有48种排法.
种排法,即共有48种排法.
[点评]本题考查了有限制条件的排列组合问题以及分类讨论思想.
33.(江苏卷)今有2个红球、3个黄球、4个白球,同色球不加以区分,将这9个球排成一列有 种不同的方法(用数字作答)。
[思路点拨]本题考查排列组合的基本知识.
[正确解答]由题意可知,因同色球不加以区分,实际上是一个组合问题,共有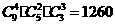
[解后反思]分步计数原理与分类计数原理是排列组合中解决问题的重要手段,也是基础方法,在高中数学中,只有这两个原理,尤其是分类计数原理与分类讨论有很多相通之处,当遇到比较复杂的问题时,用分类的方法可以有效的将之化简,达到求解的目的.
32.(湖南卷)若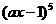 的展开式中
的展开式中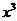 的系数是-80,则实数
的系数是-80,则实数 的值是
.
的值是
.
解: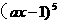 的展开式中
的展开式中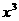 的系数
的系数 =
=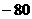 x3, 则实数
x3, 则实数 的值是-2.
的值是-2.
31.(湖北卷)安排5名歌手的演出顺序时,要求某名歌手不第一个出场,另一名歌手不最后一个出场,不同排法的总数是 .(用数字作答)
解:分两种情况:(1)不最后一个出场的歌手第一个出场,有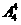 种排法(2)不最后一个出场的歌手不第一个出场,有
种排法(2)不最后一个出场的歌手不第一个出场,有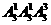 种排法,故共有78种不同排法
种排法,故共有78种不同排法
30.(湖北卷)某工程队有6项工程需要单独完成,其中工程乙必须在工程甲完成后才能进行,工程丙必须在工程乙完成后才能进行,有工程丁必须在工程丙完成后立即进行。那么安排这6项工程的不同排法种数是 。(用数字作答)
解:依题意,只需将剩余两个工程插在由甲、乙、丙、丁四个工程形成的5个空中,可得有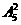 =20种不同排法。
=20种不同排法。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com