
题目列表(包括答案和解析)
7.双曲线C1: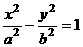 (a>0,b>0)的左准线为l,左焦点和右焦点分别为F1和F2;抛物线C2的准线为l,焦点为F2.C1和C2的一个交点为M,则
(a>0,b>0)的左准线为l,左焦点和右焦点分别为F1和F2;抛物线C2的准线为l,焦点为F2.C1和C2的一个交点为M,则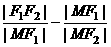 等于
等于
A.-1
B.1
C.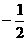 D.
D.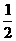
6.若数列{an}满足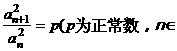 N*),则称{an}为“等方比数列”.
N*),则称{an}为“等方比数列”.
甲:数列{an}是等方比数列;乙:数列{an}是等比数列.则
A. 甲是乙的充分条件但不是必要条件
B. 甲是乙的必要条件但不是充分条件
C. 甲是乙的充要条件
D. 甲既不是乙的充分条件也不是乙的必要条件
5.已知p和q是两个不相等的正整数,且q≥2,则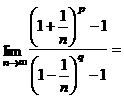
A.0
B.1
C.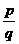 D.
D.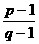
4.平面α外有两条直线m和n,如果m和n在平面α内的射影分别是m'和n',给出下列四个命题:
①m'⊥n'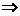 m⊥n;
②m⊥n
m⊥n;
②m⊥n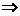 m'⊥n'
m'⊥n'
③m'与n'相交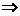 m与n相交或重合; ④m'与n'平行
m与n相交或重合; ④m'与n'平行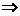 m与n平行或重合.
m与n平行或重合.
其中不正确的命题个数是
A.1 B.2 C.3 D.4
3.设P和Q是两个集合,定义集合P-Q=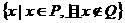 ,如果P={x|log2x<1},Q={x||x-2|<1},那么P-Q等于
,如果P={x|log2x<1},Q={x||x-2|<1},那么P-Q等于
A.{x|0<x<1} B.{x|0<x≤1} C.{x|1≤x<2} D.{x|2≤x<3}
2.将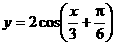 的图象按向量a=
的图象按向量a=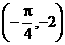 平移,则平移后所得图象的解析式为
平移,则平移后所得图象的解析式为
A.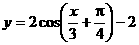 B.
B. 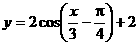
C. 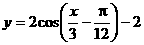 D.
D.
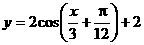
1. 如果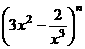 的展开式中含有非零常数项,则正整数n的最小值为
的展开式中含有非零常数项,则正整数n的最小值为
A.3 B.5 C.6 D.10
20.(本小题满分14分)
对于函数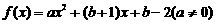 ,若存在实数
,若存在实数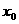 ,使
,使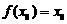 成立,则称
成立,则称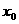 为
为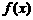 的不动点.
的不动点.
(1)当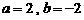 时,求
时,求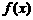 的不动点;
的不动点;
(2)若对于任何实数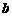 ,函数
,函数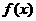 恒有两相异的不动点,求实数
恒有两相异的不动点,求实数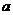 的取值范围;
的取值范围;
(3)在(2)的条件下,若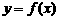 的图象上
的图象上 、
、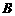 两点的横坐标是函数
两点的横坐标是函数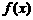 的不动点,且直线
的不动点,且直线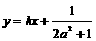 是线段
是线段 的垂直平分线,求实数
的垂直平分线,求实数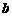 的最小值.
的最小值.
19.(本题满分14分)
设函数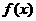 =
=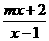 的图象关于直线
的图象关于直线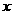 -
-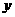 =0对称.
=0对称.
(1)求 的值;
的值;
(2)判断并证明函数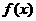 在区间(1,+∞)上的单调性;
在区间(1,+∞)上的单调性;
(3)若直线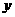 =
=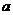 (
(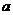 ∈R)与
∈R)与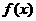 的图象无公共点,且
的图象无公共点,且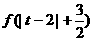 <2
<2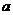 +
+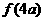 ,求实数
,求实数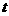 的取值范围.
的取值范围.
18. (本小题满分14分)
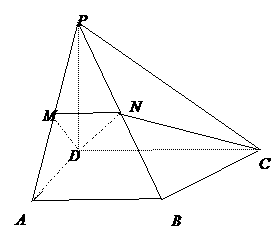 如图,四棱锥
如图,四棱锥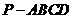 中,
中,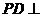 底面
底面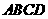 ,
,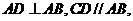 且
且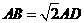 ,
,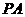 与
与
底面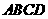 成
成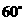 角,点
角,点 分别是
分别是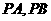 的中点.
的中点.
(Ⅰ)求证: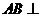 平面
平面 ;
;
(Ⅱ)求二面角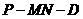 的大小;
的大小;
(Ⅲ)当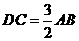 时,求异面直线
时,求异面直线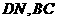 所成的角.
所成的角.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com