
题目列表(包括答案和解析)
19.双曲线的中心是原点O,它的虚轴长为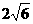 ,相应于焦点F(c,0)(c>0)的准线l与x轴交于点A,且| OF |= 3 | OA |。过点F的直线与双曲线交于P、Q两点。
,相应于焦点F(c,0)(c>0)的准线l与x轴交于点A,且| OF |= 3 | OA |。过点F的直线与双曲线交于P、Q两点。
(Ⅰ)求双曲线的方程及离心率;(Ⅱ)若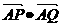 =0,求直线PQ的方程。
=0,求直线PQ的方程。
18.已知函数f(x)=(x2+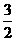 )(x+a)(a
)(x+a)(a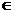 R)
R)
(1)若函数f(x)的图象上有与x轴平行的切线,求a的范围;
(2)若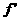 (-1)=0,(I)求函数f(x)的单调区间;(II)证明对任意的x1、x2
(-1)=0,(I)求函数f(x)的单调区间;(II)证明对任意的x1、x2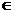 (-1,0),不等式|f(x1)-f(x2)|<
(-1,0),不等式|f(x1)-f(x2)|<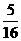 恒成立。
恒成立。
17.已知抛物线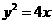 上两定点A、B分别在对称轴两侧,F为焦点,且
上两定点A、B分别在对称轴两侧,F为焦点,且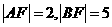 ,在抛物线的AOB一段上求一点P,使
,在抛物线的AOB一段上求一点P,使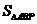 最大,并求面积最大值。
最大,并求面积最大值。
16.有红蓝两粒质地均匀的正方体形状骰子,红色骰子有两个面是8,四个面是2,蓝色骰子有三个面是7,三个面是1,两人各取一只骰子分别随机投掷一次,所得点数较大者获胜. ⑴分别求出两只骰子投掷所得点数的分布列及期望;⑵投掷蓝色骰子者获胜的概率是多少?
15. 已知向量 =(sinB,1-cosB),且与向量
=(sinB,1-cosB),且与向量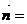 (2,0)所成角为
(2,0)所成角为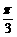 ,其中A, B, C是⊿ABC的内角.
,其中A, B, C是⊿ABC的内角.
(1)求角B的大小;
(2)求sinA+sinC的取值范围.
14.椭圆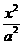 +
+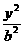 =1(a>b>0)上两点A,B与中心O的连线互相垂直,则
=1(a>b>0)上两点A,B与中心O的连线互相垂直,则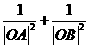 =
=
13.若点A(1,2)和B(1,1)在直线3x-y+m=0的异侧,则m的取值范围是______________
12.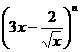 的展开式中第9项是常数项,n的值是
的展开式中第9项是常数项,n的值是
11.若圆锥曲线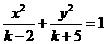 的焦距与k无关,则它的焦点坐标是__________.
的焦距与k无关,则它的焦点坐标是__________.
10.由正方体的八个顶点中的两个所确定的所有直线中,取出两条,这两条直线是异面直线的概率为 ( )
A. 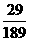 B.
B. 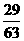 C.
C. 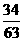 D.
D. 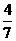
第Ⅱ卷(选择题 共100分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com